Формы КС-2 и КС-3 что это и зачем они нужны
Если вы часто являетесь одной из сторон правовых отношений, в которых предметом договора выступают строительно-монтажные работы, вы уже знаете, что все расчеты между сторонами и урегулирование спорных вопросов ведутся на основании определенных документов. Но среди участников рынка строительных услуг, заказывающих их один раз в 5-10 лет и реже, есть те, кто даже не знает, что такое формы КС-2 и КС-3.
Унифицированные бланки не всегда, конечно, обязательны к применению. Даже если подрядчик оформит выполненную работу актами в свободной форме, то при возникновении недоразумений сможет доказать правомерность своих требований. И все же, давайте попробуем разобраться и понятным языком объяснить, что это за бланки, для чего их нужно заполнять и как они могут обеспечить взаимопонимание между заказчиком работ и исполнителем.
Цель составления форм КС-2 и КС-3
Заключая договор о выполнении строительно-монтажных работ, не стоит упускать из вида документацию, которая в обязательном порядке должна заполняться и подписываться всеми участниками сделки.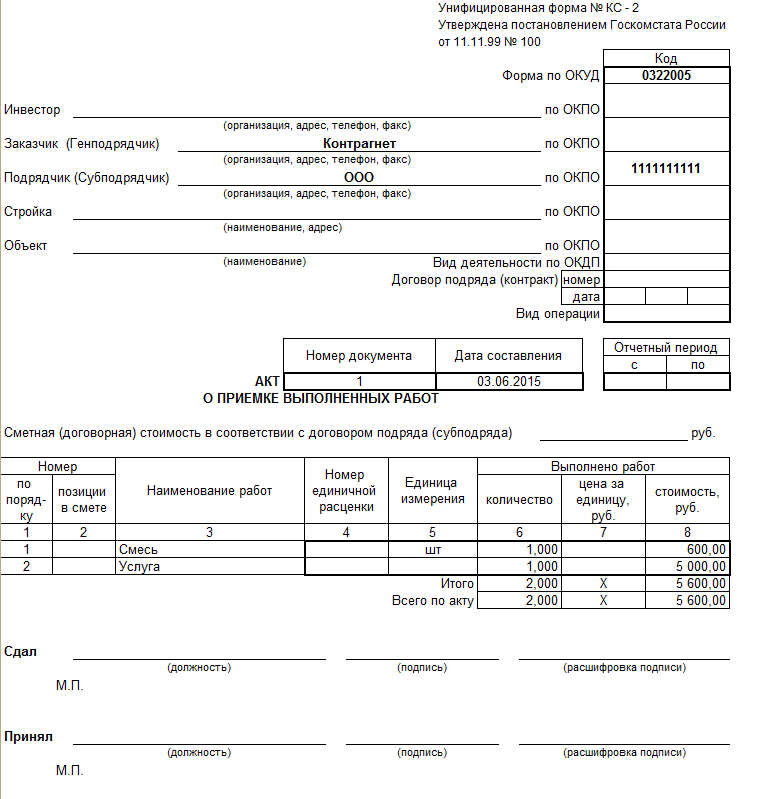
Основным документом, по которому оплачиваются выполненные обязательства, промежуточная и конечная сумма по этапам строительства, является Акт о приемке выполненных работ (КС-2). Все выполненные объемы фиксируются в Журнале учета выполненных работ, поэтому составление акта выполняется на основании записей, внесенных в такой Журнал.
Все строительно-монтажные операции осуществляются в соответствии с составленной ранее и утвержденной до подписания договора сметы. Это один из главных документов, согласованный получателем ремонтно-строительных услуг, на основании которого подрядчик имеет право вносить в журнал учета перечень выполненных работ.
По сути, форма КС-3 – Справка о стоимости выполненных работ и затрат – это документ, дублирующий Акт, однако в этом бланке учитываются:
- отклонения в стоимости материалов;
- повышение заработной платы строителей;
- вызов спецтехники, сопряженный с возникновением дополнительного или неучтенного объема операций;
- затраты, согласованные заказчиком, но неучтенные в смете;
- другие незапланированные расходы.

Если вы не знаете, как составлять формы КС-2 и КС-3, лучше обратиться в специализированную компанию, для которой заполнение этих документов – привычное дело. Имейте в виду, что правильно составленная документация – правомерное основание требовать оплату за оказанные услуги и выполненные строительно-монтажные работы. Только при составлении и подписании сторонами в количестве, оговоренном в договоре, документация имеет правовую силу.
Форма КС-2, бланк КС2, акт КС 2
При документальном оформлении выполненных работ (оказанных услуг) организация использует унифицированные формы актов или же формы актов, утвержденные соответствующими нормативно-правовыми актами.
В капитальном строительстве для оформления выполненных работ применяются типовые формы первичных документов, утвержденные постановлением Росстатагентства России от 11 ноября 1999 г. N 100 «Об утверждении унифицированных форм первичной учетной документации по учету работ в капитальном строительстве и ремонтно-строительных работ», а именно «Акт о приемке работ» (форма N КС-2) и «Справка о стоимости выполненных работ и затрат» (форма N КС-3).
Акт о приемке выполненных работ (форма N КС-2)
применяется для приемки выполненных подрядных строительно-монтажных работ производственного, жилищного, гражданского и других назначений. Акт составляется на основании данных Журнала учета выполненных работ (форма N КС-6а в необходимом количестве экземпляров. Акт подписывается уполномоченными представителями сторон, имеющих право подписи (производителя работ и заказчика (генподрядчика).На основании данных Акта о приемке выполненных работ заполняется Справка о стоимости выполненных работ и затрат (форма N КС-3).
В указанных формах документов содержатся измерители хозяйственной операции — рубли. Поэтому заполнение указанных форм в иностранной валюте будет являться нарушением требований законодательства Российской Федерации, предъявляемых к первичным учетным документам.
В соответствии с положениями статьи 745 ГК РФ обязанность по обеспечению строительства материалами, деталями, конструкциями или оборудованием может быть возложена в том числе и на заказчика.
Подрядная организация со своей стороны обязана в соответствии со статьей 713 ГК РФ после окончания работ представить заказчику отчет об израсходовании материалов, возвратить их остаток либо с согласия заказчика уменьшить цену работ с учетом стоимости остающегося в распоряжении подрядчика неиспользованного материала.
Акт о приемке выполненных работ составляют, когда подрядчик (субподрядчик) выполнил строительно-монтажные работы и заказчик (генподрядчик) не имеет к ним претензий. Затем данные из этого документа подрядчик переносит в Справку о стоимости выполненных работ и затрат (форма N КС-3). А заказчик на основании этой справки расплачивается с ним. Акт можно составлять и после каждого этапа работ, если в договоре предусмотрено, что строительство ведется в несколько этапов.
См. также:
Оформить акт КС-2
Образец формы КС-2 — pdf
Образец формы КС-2 — gifВопросы и ответы по форме
Что такое КС-2 и КС-3?
Акт о приемке выполненных работ
Применяется для приемки выполненных подрядных строительно-монтажных работ производственного, жилищного, гражданского и других назначений. Акт составляется на основании сметы (ведомость объемов и стоимости работ, протокол согласования договорной цены) которая как правило является Приложением к Договору подряда между Заказчиком (Генподрядчиком) и Подрядчиком (Субподрядчиком). Форма КС-2 составляется в необходимом количестве экземпляров, обычно 2 (два), но точное количество указывается в Договоре подряда. Форма КС-2 подписывается уполномоченными представителями сторон, имеющих право подписи (Подрядчика (Субподрядчика) и Заказчика (Генподрядчика).
На основании данных Акта о приемке выполненных работ (форма КС-2) заполняется Справка о стоимости выполненных работ и затрат (форма N КС-3).
Справка о стоимости выполненных работ
Применяется для расчетов с Заказчиком за выполненные работы. Справка составляется в необходимом количестве экземпляров. Один экземпляр — для Подрядчика (Субподрядчика), второй — для Заказчика (Застройщика, Генподрядчика). В адрес финансирующего банка и инвестора Справка представляется только по их требованию.
Выполненные работы и затраты в Справке отражаются исходя из договорной стоимости.
Справка по форме КС-3 составляется на выполненные в отчетном периоде строительные и монтажные работы, работы по капитальному ремонту зданий и сооружений, другие подрядные работы и представляется Субподрядчиком Генподрядчику, Генподрядчиком Заказчику (Застройщику).
В стоимость выполненных работ и затрат включается стоимость строительно-монтажных работ, предусмотренных сметой, а также прочие затраты, не включаемые в единичные расценки на строительные работы и в ценники на монтажные работы (рост стоимости материалов, заработной платы, тарифов, расходов на эксплуатацию машин и механизмов, дополнительные затраты при производстве работ в зимнее время, средства на выплату надбавок за подвижной и разъездной характер работы, надбавки за работу на Крайнем Севере и в приравненных к нему районах, изменение условий организации строительства и т. п.).
п.).
В графе 4 стоимость работ и затрат указываются нарастающим итогом с начала выполнения работ, включая отчетный период.
В графе 5 стоимость работ и затрат указываются нарастающим итогом с начала года, включая отчетный период.
В графе 6 выделяются данные за отчетный период.
Данные приводятся в целом по стройке, с выделением данных по каждому входящему в ее состав объекту (пусковому комплексу, этапу).
В Справке по требованию заказчика или инвестора приводятся данные по видам оборудования, относящегося к стройке (пусковому комплексу, этапу), к монтажу которого приступили в отчетном периоде. При этом в графе 2 указываются наименование и модель оборудования, а в графах 4, 5, 6 — данные о выполненных монтажных работах.
По строке «Итого» отражается итоговая сумма работ и затрат без учета НДС.
Отдельной строкой указывается сумма НДС.
По строке «Всего» указывается стоимость выполненных работ и затрат с учетом НДС.
КС-2 — образец заполнения формы в 2020 и 2021 году
Бланк унифицированной формы КС-2
Акт о приемке выполненных работ — форма КС-2, бланк, образец заполнения которой вы сможете скачать в статье, утвержден Постановлением Госкомстата № 100 от 11.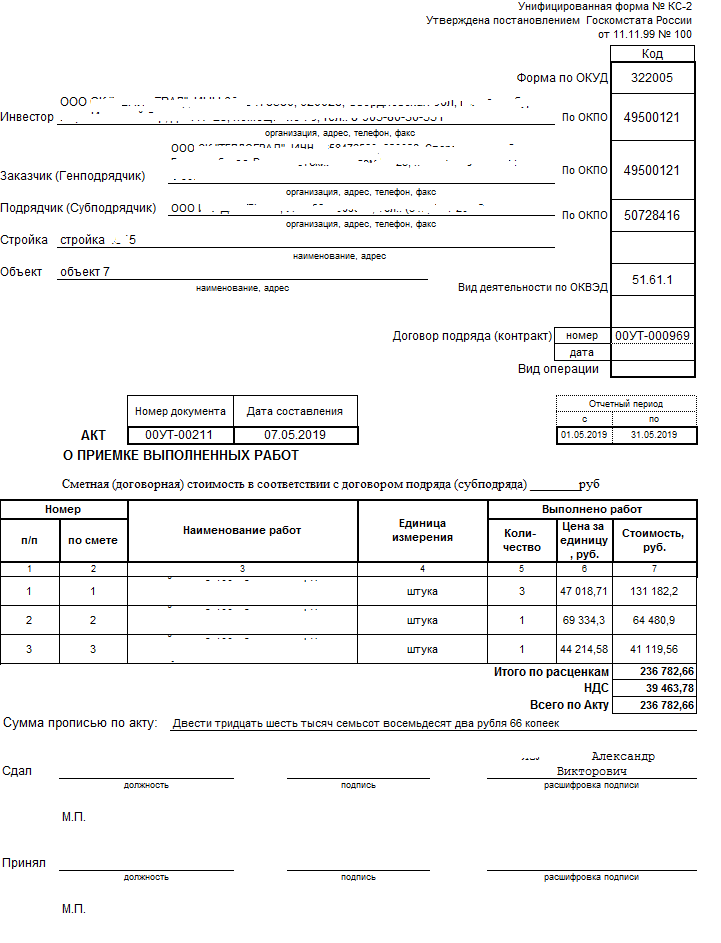
Согласно Письму Росстата № 01-02-9/381, заполнение акта является строго обязательным для каждого исполнителя. На основании КС-2 исполнитель сдает, а заказчик принимает строительно-монтажные и ремонтные работы на объектах жилищного, производственного и гражданского характера. Таким образом, подписав акт КС-2, он подтверждает отсутствие претензий к качеству и объему выполненных работ. В статье вы сможете скачать образец заполнения КС-2 в 2020 году.
Как заполнять
Мы приведем образец заполнения формы КС-2 и КС-3, скачать excel 2020 года можно бесплатно.
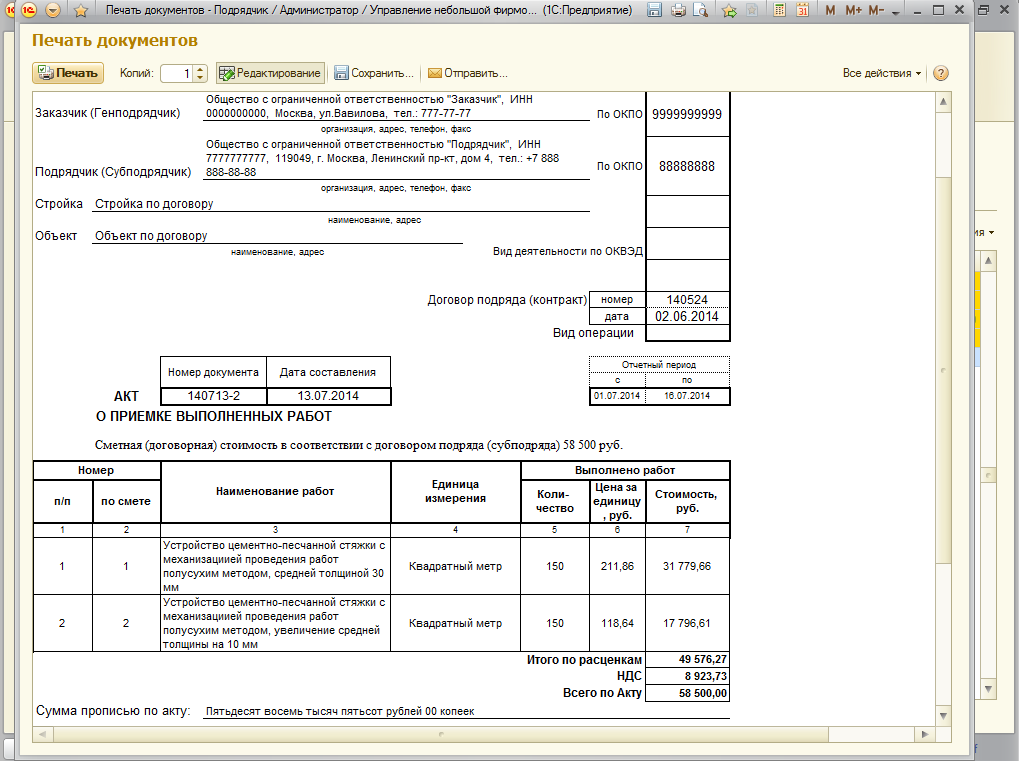
Начнем с первой из них — форма КС-2, образец заполнения 2020 года будет следующий. В первую очередь оформляется титульная часть документа:
В первую очередь оформляется титульная часть документа:
- унифицированная форма КС-2 имеет код по ОКУД — 0322005;
- строки «Инвестор» (при наличии), «Заказчик» и «Подрядчик» заполняются в соответствии с точными юридическими данными об организациях: полное наименование, организационно-правовая форма, юридический адрес, номера телефонов, факса, ОКПО;
- в поле «Стройка» вносится название стройки и ее адрес, а в позиции «Объект» — полное наименование строительного объекта;
- далее вносится вид деятельности по ОКДП в КС-2;
- указываются номер и дата (ДД.ММ.ГГГГ) договора (контракта) в соответствующей графе;
- проставляются номер и дата формирования бланка, а также отчетный период по вышеуказанному контракту;
- прописывается сметная стоимость ремонта, монтажа, строительства, которые выполнял подрядчик и по которым отчитывается перед заказчиком в соответствии с заключенным контрактом. Сумма должна быть указана в рублях.

Продолжаем разбираться, как заполнить КС-2, пример заполнения табличной части документа будет выглядеть следующим образом. Уточняем, как заполнять отдельно в каждый столбец:
- Порядковые номера.
- «Номер позиции по смете» — нумерация выполняемой работы или используемого материала на основании сметной документации. Если бланк заполняется в соответствии с несколькими сметами, то нумерация может дублироваться.
- Когда составляется форма КС-2, образец заполнения требует, чтобы наименование каждого пункта было строго в соответствии со сметной документацией.
- «Номер единичной расценки» — шифры из сметы на базе сборников ФЕР.
- «Единица измерения» — указывается качественное обозначение выполненных действий по договору подряда.
- В этом столбце вносится количественное обозначение подрядных действий. Запрещено указывать долю выполнения в процентах.
- Столбец 7 включает данные о цене за единицу на основании сборников единичных расценок.
 Если цены по контракту фиксированные, то в столбце проставляются прочерки.
Если цены по контракту фиксированные, то в столбце проставляются прочерки. - Последняя колонка заполняется в любом случае. В ней указывается стоимость подрядных работ либо в соответствии с контрактом, либо на основе рассчитанного показателя из сборников ФЕР.
Если у представителей организации-заказчика были установлены замечания к срокам, объемам или качеству выполненных работ, их также необходимо зафиксировать в акте КС-2, как правильно заполнить образец которого вы теперь знаете.
Готовая форма КС-2 — акт о приемке выполненных работ — подписывается руководителями подрядчика и заказчика (после проверки и согласования). Для согласования необходимо предоставить справку по форме КС-3. В статье вы можете КС-2, КС-3 (образец заполнения в 2020 году) скачать бесплатно в excel.
Заполнение формы КС-2: пример заполнения
Бланк формы КС-3
Мы рассмотрели заполнение формы КС-2, пример заполнения КС-3 рассмотрим далее. Используется унифицированная форма ОКУД под номером 0322001. При заполнении нельзя менять форму, например, количество строк!
При заполнении нельзя менять форму, например, количество строк!
Скачать
Как заполнять справку КС-3
Акты КС-2 и КС-3, образец заполнения для которых мы приводим в статье, оформляют на этапе закрытия контракта. КС-3 заполняется в двух экземплярах на основании госконтракта и акта КС-2, образец заполнения 2020 года для которого мы описали выше. Если в строительстве задействована третья сторона, например инвестор, то подрядчик готовит документ и для нее. В статье приводится унифицированная форма КС-2 и КС-3, образец заполнения, инструкция по заполнению. Они помогут не допустить ошибок.
В справку вносят данные по стоимости и затратам выполненного ремонта, монтажа, строительства, а также издержки, которые не учли в сметной документации и контракте. Это может быть, например, непредвиденный рост цен на аренду оборудования или на стройматериалы. Справку можно заполнить не только ко всему строительному объекту, но и к отдельной его части. В этом случае нужно указать полную стоимость всего объекта.
Шаг 1. Титульный лист.
Форма КС-2 и КС-3, образец заполнения которых мы рассматриваем, начинают заполняться с титульной части.
Нужно внести:
- данные заказчика, исполнителя и при необходимости — инвестора. Указываются полное наименование и контактные данные;
- код по ОКПО;
- наименование и адрес объекта строительства;
- реквизиты госконтракта;
- актуальный номер и дата справки;
- отчетный период, в котором велись работы.
Шаг 2. Заполняем таблицу.
Как и в случае с КС-2, образец заполнения в 2020 году для справки КС-3 продолжается заполнением табличной части. Внимательно внесите данные по следующим столбцам:
- Порядковый номер.
- Описание работ и объекта или его этапа, а также оборудования и материалов. Если позволяет контракт и документация, можно разделить выполненные работы по типам применяемого техоборудования.
- Код видов работ.

- Цена с нарастающим итогом.
- Стоимость, определенная исполнителем в начале отчетного периода (года).
- Итоговая стоимость выполненного подряда за отчетный период.
В конце табличной части заполняются строки «Итого» — окончательная сумма произведенного строительства, а также стоимость с учетом НДС. На этом образец заполнения КС-2 и КС-3 можно считать законченным.
Шаг 3. Заверяем документ.
В конце документа должны подписаться ответственные лица со стороны заказчика и исполнителя. Также справку нужно заверить печатями организаций.
Мы рассмотрели заполнение КС-2 и КС-3, образец заполнения последней вы можете скачать ниже.
Образец заполнения справки КС-3
|
Консоли кабельные КС1, КС2, КС3 предназначены для установки лотков, коробов, а также для открытой прокладки кабелей и проводов в трубах и кожухах по стенам строительных конструкций с помощью анкеров. Общее описание консолей кабельных КС1, КС2, КС3Консоли кабельные КС1, КС2, КС3 изготавливаются c антикоррозионными покрытиями для различных климатических условий. Наиболее заказываемыми являются консоли, изготовленные из оцинкованного листа КС1цУТ1,5/ КС2цУТ1,5/ КС3цУТ1,5 и покрытые порошковой краской. При заказе консолей КС1, КС2, КС3 с порошковой окраской можно выбрать цвет согласно таблицы RAL. Внешне консоли кабельные КС1 и КС2 имеют массу сходств: общая длина консоли (L), высота установочной пластины 146,0 мм, двойная перфорация. Только один размер имеет отличие — ширина установочной пластины (B), у консоли КС1 на 5,0 мм больше, чем у консоли КС2. Различие связано, прежде всего, с местом монтажа. Увеличение ширины установочной пластины (B) — дает увеличение точки опоры, консоль кабельную КС1 устанавливают на стены при помощи анкеров.
|
Каким актом (по форме КС-2 или обычным, составленным в произвольной форме) оформлять исполнение договора на выполнение проектных работ и проектно-изыскательских работ?
Скачать форму акта.
Рассмотрев вопрос, мы пришли к следующему выводу:
По нашему мнению, при выполнении проектных работ нет необходимости применять акт о приемке выполненных работ (форма N КС-2). Завершение работ может быть оформлено актом выполненных работ, составленным в соответствии с требованиями законодательства.
Обоснование вывода:
Исходя из п. 2 ст. 720 ГК РФ сдача-приемка выполненных работ по договору подряда фиксируются в акте либо в ином соответствующем документе, подписанном обеими сторонами.
Данная норма, в силу п. 2 ст. 702 ГК РФ, применяется и к договору на выполнение проектных работ и проектно-изыскательских работ.
А поскольку исходя из п. 1 ст. 702, ст. 711 ГК РФ оплата работ по договору подряда производится на основании приемки этих работ, оформляемых соответствующим актом, то данный акт является и основанием для оплаты, то есть первичным учетным документом.
В соответствии с требованиями п. 1 и п. 2 ст. 9 Федерального закона от 21.11.1996 N 129-ФЗ «О бухгалтерском учете» (далее — Федеральный закон N 129-ФЗ) все хозяйственные операции, проводимые организацией, должны оформляться оправдательными документами. Они служат первичными учетными документами, на основании которых ведется бухгалтерский учет.
Первичные учетные документы принимаются к учету, если они составлены по форме, содержащейся в альбомах унифицированных форм первичной учетной документации, а документы, форма которых не предусмотрена в этих альбомах, должны содержать перечень обязательных реквизитов, установленный ст. 9 Федерального закона N 129-ФЗ.
Унифицированная форма акта о приемке выполненных проектных работ не утверждена.
Унифицированная форма первичной учетной документации КС-2 «Акт о приемке выполненных работ», утвержденная постановлением Российского статистического агентства от 11.11.1999 N 100 «Об утверждении унифицированных форм первичной учетной документации по учету работ в капитальном строительстве и ремонтно-строительных работ», в соответствии с Указаниями по применению унифицированных форм, содержащимися в этом же постановлении, применяется для приемки выполненных подрядных строительно-монтажных работ производственного, жилищного, гражданского и других назначений.
Термин «строительно-монтажные работы» в действующем законодательстве отсутствует. В письме Минфина России от 05.11.2003 N 04-03-11/91 высказано мнение, что «строительно-монтажные работы для целей применения НДС следует рассматривать как работы капитального характера, в результате которых создаются новые объекты основных средств, в том числе объекты недвижимого имущества (здания, сооружения и т.п.), или изменяется первоначальная стоимость данных объектов, находящихся в эксплуатации, в случаях достройки, дооборудования, реконструкции, модернизации, технического перевооружения, частичной ликвидации и по иным аналогичным основаниям».
Если руководствоваться указанной позицией, то проектные и проектно-изыскательские работы в буквальном смысле не являются строительно-монтажными. Следовательно, при выполнении по договору подряда необходимости применять форму КС-2 нет.
Существующая арбитражная практика также подтверждает, что применение формы КС-2 для приемки проектных работ не обязательно. Аргументируется это тем, что «спецификой данного договора является разработка проектной документации; акты о приемке выполненных работ формы КС-2 являются унифицированной формой первичной учетной документации по учету работ в капитальном строительстве и ремонтно-строительных работах» (постановления ФАС Дальневосточного округа от 26.09.2006 N Ф03-А51/06-1/3095 и от 12.07.2007 N Ф03-А51/07-1/1866 (определением ВАС РФ от 27.09.2007 N 11311/07 в передаче последнего дела в Президиум ВАС РФ для пересмотра в порядке надзора отказано), постановление ФАС Московского округа от 26.06.2009 N КГ-А40/4264-09).
Аргументируется это тем, что «спецификой данного договора является разработка проектной документации; акты о приемке выполненных работ формы КС-2 являются унифицированной формой первичной учетной документации по учету работ в капитальном строительстве и ремонтно-строительных работах» (постановления ФАС Дальневосточного округа от 26.09.2006 N Ф03-А51/06-1/3095 и от 12.07.2007 N Ф03-А51/07-1/1866 (определением ВАС РФ от 27.09.2007 N 11311/07 в передаче последнего дела в Президиум ВАС РФ для пересмотра в порядке надзора отказано), постановление ФАС Московского округа от 26.06.2009 N КГ-А40/4264-09).
Следовательно, поскольку унифицированной формы акта о приемке выполненных проектных работникам нет, то сдача-приемка этих работ могут быть оформлены актом приемки выполненных работ, составленным в свободной форме с соблюдением обязательных требований, установленных ст. 9 Федерального закона N 129-ФЗ.
В то же время сложившаяся практика показывает, что стороны договора подряда на выполнение проектных работ в качестве акта, подтверждающего приемку выполненных проектных работ, могут (но не обязаны) использовать форму КС-2 (постановления ФАС Центрального округа от 17. 11.2009 N А14-633/2009/23/36, ФАС Уральского округа от 23.09.2009 N Ф09-7292/09-С4, ФАС Западно-Сибирского округа от 07.09.2009 N Ф04-5295/2009).
11.2009 N А14-633/2009/23/36, ФАС Уральского округа от 23.09.2009 N Ф09-7292/09-С4, ФАС Западно-Сибирского округа от 07.09.2009 N Ф04-5295/2009).
Ответ подготовил:
Эксперт службы Правового консалтинга ГАРАНТ
Лазукова Екатерина
Контроль качества ответа:
Рецензент службы Правового консалтинга ГАРАНТ
Серков Аркадий
21 сентября 2010 г.
Материал подготовлен на основе индивидуальной письменной консультации, оказанной в рамках услуги Правовой консалтинг.
Смесительная камера КС
| Характеристики | ВС-1110 + КС1 | ВС-1220 + КС1 | ВС-1230 + КС1 | ВС-2125 + КС2 | ВС-2245 + КС2 | ВС-2365 + КС2 |
| Производительность (м3/ч) | 800-1750 | 550-1600 | 300-1500 | 1600-3200 | 1250-3000 | 1000-2800 |
| Тепловая мощность (кВт) | 6,0-9,2 | 9,3-18,7 | 6,9-23,3 | 15,2-24,2 | 20,9-37,3 | 24-52 |
| Корпус | сталь + алюминий + пластик | |||||
| Цвет | серебристый | |||||
| Вес оборудования, наполненного водой (кг) | 26,6 | 24,7 | 28 | 35,3 | 37,5 | 40,5 |
| Вес (кг) | 25,9 | 24 | 26,8 | 34,4 | 35,5 | 37,8 |
| Присоединительные патрубки | ¾ “ | |||||
| Максимальная длина струи воздуха (м) | 12 | 11 | 10 | 18 | 16,5 | 15,5 |
| Макс. уровень акустического давления дб (А) | 47 | 54 | ||||
| КС 1 | КС 2 |
Монтажная консоль При помощи монтажной консоли можно установить оборудование перпендикулярно к стене. | ||
| Рекомендуемые расстояния установки | ||
| КС 1 | КС 2 | |
| А, м | 2,5–3.0 | 2,5–6,0 |
| В, м* | 2.4–4.5 | 2,5–8,0 |
* При подборе надо учесть длину потока неизотермического воздуха.
К смесительным камерам КС применяется система управления КС-У, которая обеспечивает питание, управление и защиту для одного водяного тепловентилятора, работающего совместно со смесительной камерой. Автоматика для камер смешения включает в себя следующие элементы:
| Схема подключения камер смешения ГРЕЕРС КС к командоконтроллеру T-Box |
Решайте неравенства с помощью программы «Пошаговое решение математических задач»
В этой главе мы разработаем определенные методы, которые помогут решить проблемы, сформулированные на словах. Эти методы включают переписывание задач в виде символов. Например, заявленная проблема
«Найдите число, которое при добавлении к 3 дает 7»
можно записать как:
3+? = 7, 3 + n = 7, 3 + x = 1
и так далее, где символы?, N и x представляют число, которое мы хотим найти.Мы называем такие сокращенные версии поставленных задач уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку переменная имеет показатель степени 1. Члены слева от знака равенства составляют левую часть уравнения; те, что справа, составляют правую часть. Таким образом, в уравнении x + 3 = 7 левый член равен x + 3, а правый член равен 7.
РЕШЕНИЕ УРАВНЕНИЙ
Уравнения могут быть истинными или ложными, так же как словесные предложения могут быть истинными или ложными.Уравнение:
3 + х = 7
будет ложным, если вместо переменной подставлено любое число, кроме 4. Значение переменной, для которой верно уравнение (4 в этом примере), называется решением уравнения. Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.
Пример 1 Определите, является ли значение 3 решением уравнения
4x — 2 = 3x + 1
Решение Мы подставляем значение 3 вместо x в уравнение и смотрим, равен ли левый член правому.
4 (3) — 2 = 3 (3) + 1
12 — 2 = 9 + 1
10 = 10
Отв. 3 — это решение.
Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем осмотра.
Пример 2 Найдите решение каждого уравнения путем осмотра.
а. х + 5 = 12
б. 4 · х = -20
Решения а. 7 — решение, так как 7 + 5 = 12.
b. -5 — это решение, поскольку 4 (-5) = -20.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИСЛЕНИЯ
В разделе 3.1 мы решили путем проверки несколько простых уравнений первой степени. Однако решения большинства уравнений не сразу видны при осмотре. Следовательно, нам нужны некоторые математические «инструменты» для решения уравнений.
ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ
Эквивалентные уравнения — это уравнения, которые имеют идентичные решения. Таким образом,
3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5
— эквивалентные уравнения, потому что 5 — единственное решение каждого из них.Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не очевидно при осмотре, но в уравнении x = 5 решение 5 очевидно при осмотре. Решая любое уравнение, мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить.
Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов создания эквивалентных уравнений.
Если одно и то же количество добавляется или вычитается из обоих элементов уравнения, полученное уравнение эквивалентно исходному уравнение.
в символах,
a — b, a + c = b + c и a — c = b — c
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
х + 3 = 7
путем вычитания 3 из каждого члена.
Решение Если вычесть 3 из каждого члена, получится
х + 3 — 3 = 7 — 3
или
х = 4
Обратите внимание, что x + 3 = 7 и x = 4 — эквивалентные уравнения, поскольку решение одинаково для обоих, а именно 4.В следующем примере показано, как мы можем генерировать эквивалентные уравнения, сначала упростив один или оба члена уравнения.
Пример 2 Напишите уравнение, эквивалентное
4x- 2-3x = 4 + 6
, объединив одинаковые термины, а затем добавив по 2 к каждому члену.
Объединение одинаковых терминов дает
х — 2 = 10
Добавление 2 к каждому члену дает
х-2 + 2 = 10 + 2
х = 12
Чтобы решить уравнение, мы используем свойство сложения-вычитания, чтобы преобразовать данное уравнение в эквивалентное уравнение вида x = a, из которого мы можем найти решение путем проверки.
Пример 3 Решить 2x + 1 = x — 2.
Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала прибавим -1 к каждому члену (или вычтем 1 из него), мы получим
.2x + 1-1 = x — 2-1
2x = х — 3
Если мы теперь прибавим -x к каждому члену (или вычтем x из него), мы получим
2х-х = х — 3 — х
х = -3
, где решение -3 очевидно.
Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3.
Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2. В приведенном выше примере мы можем проверить решение, подставив — 3 вместо x в исходном уравнении.
2 (-3) + 1 = (-3) — 2
-5 = -5
Симметричное свойство равенства также помогает при решении уравнений. В этом объекте указано
Если a = b, то b = a
Это позволяет нам менять местами члены уравнения в любое время, не беспокоясь о каких-либо изменениях знака.Таким образом,
Если 4 = x + 2, то x + 2 = 4
Если x + 3 = 2x — 5, то 2x — 5 = x + 3
Если d = rt, то rt = d
Может быть несколько разных способов применить свойство сложения, указанное выше. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства.
Пример 4 Решите 2x = 3x — 9. (1)
Решение Если мы сначала добавим -3x к каждому члену, мы получим
2x — 3x = 3x — 9 — 3x
-x = -9
, где переменная имеет отрицательный коэффициент.Хотя при осмотре мы можем видеть, что решение равно 9, поскольку — (9) = -9, мы можем избежать отрицательного коэффициента, добавив -2x и +9 к каждому члену уравнения (1). В этом случае получаем
2x-2x + 9 = 3x- 9-2x + 9
9 = х
, из которого решение 9 очевидно. При желании последнее уравнение можно записать как x = 9 по симметричному свойству равенства.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВА DIVISION
Рассмотрим уравнение
3x = 12
Решение этого уравнения — 4.Также обратите внимание, что если мы разделим каждый член уравнения на 3, мы получим уравнения
, решение которого также равно 4. В общем, мы имеем следующее свойство, которое иногда называют свойством деления.
Если оба члена уравнения делятся на одно и то же (ненулевое) количество, полученное уравнение эквивалентно исходному уравнению.
в символах,
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
-4x = 12
, разделив каждый член на -4.
Решение Разделив оба элемента на -4, получим
При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, в которых переменная имеет коэффициент 1.
Пример 2 Решите 3y + 2y = 20.
Сначала мы объединяем одинаковые термины, чтобы получить
5лет = 20
Тогда, разделив каждый член на 5, получим
В следующем примере мы используем свойство сложения-вычитания и свойство деления для решения уравнения.
Пример 3 Решить 4x + 7 = x — 2.
РешениеСначала мы добавляем -x и -7 к каждому члену, чтобы получить
4x + 7 — x — 7 = x — 2 — x — 1
Далее, объединяя одинаковые термины, получаем
3x = -9
Наконец, мы разделим каждый член на 3, чтобы получить
РЕШЕНИЕ УРАВНЕНИЙ С СВОЙСТВОМ УМНОЖЕНИЯ
Рассмотрим уравнение
Решение этого уравнения — 12. Также обратите внимание, что если мы умножим каждый член уравнения на 4, мы получим уравнения
, решение которого также равно 12.В общем, мы имеем следующее свойство, которое иногда называют свойством умножения.
Если оба члена уравнения умножаются на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению.
в символах,
a = b и a · c = b · c (c ≠ 0)
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
путем умножения каждого члена на 6.
Решение Умножение каждого члена на 6 дает
При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, не содержащих дробей.
Пример 2 Решить
Решение Во-первых, умножьте каждый член на 5, чтобы получить
Теперь разделите каждый член на 3,
Пример 3 Решить.
Решение Во-первых, упростите над дробной чертой, чтобы получить
Затем умножьте каждый член на 3, чтобы получить
Наконец, разделив каждого члена на 5, получим
ДАЛЬНЕЙШИЕ РЕШЕНИЯ УРАВНЕНИЙ
Теперь мы знаем все методы, необходимые для решения большинства уравнений первой степени.Не существует определенного порядка, в котором следует применять свойства. Может оказаться подходящим любой один или несколько из следующих шагов, перечисленных на странице 102.
Шаги по решению уравнений первой степени:
- Объедините одинаковые члены в каждом члене уравнения.
- Используя свойство сложения или вычитания, запишите уравнение со всеми членами, содержащими неизвестное в одном члене, и всеми членами, не содержащими неизвестное в другом.
- Объедините одинаковые термины в каждом элементе.
- Используйте свойство умножения для удаления дробей.
- Используйте свойство деления, чтобы получить коэффициент 1 для переменной.
Пример 1 Решите 5x — 7 = 2x — 4x + 14.
Решение Во-первых, мы объединяем одинаковые члены, 2x — 4x, чтобы получить
5x — 7 = -2x + 14
Затем мы добавляем + 2x и +7 к каждому члену и объединяем одинаковые термины, чтобы получить
5x — 7 + 2x + 7 = -2x + 14 + 2x + 1
7x = 21
Наконец, мы разделим каждый член на 7, чтобы получить
В следующем примере мы упрощаем над дробной чертой перед применением свойств, которые мы изучали.
Пример 2 Решить
Решение Сначала мы объединяем одинаковые термины, 4x — 2x, чтобы получить
Затем мы добавляем -3 к каждому члену и упрощаем
Затем мы умножаем каждый член на 3, чтобы получить
Наконец, мы разделим каждый член на 2, чтобы получить
РЕШЕНИЕ ФОРМУЛ
Уравнения, в которых используются переменные для измерения двух или более физических величин, называются формулами. Мы можем найти любую из переменных в формуле, если известны значения других переменных.Мы подставляем известные значения в формулу и решаем неизвестную переменную методами, которые мы использовали в предыдущих разделах.
Пример 1 В формуле d = rt найти t, если d = 24 и r = 3.
Решение Мы можем найти t, заменив 24 на d и 3 на r. То есть
d = rt
(24) = (3) т
8 = т
Часто бывает необходимо решить формулы или уравнения, в которых есть более одной переменной для одной из переменных в терминах других.Мы используем те же методы, что и в предыдущих разделах.
Пример 2 В формуле d = rt найдите t через r и d.
Решение Мы можем решить для t в терминах r и d, разделив оба члена на r, чтобы получить
из которых по закону симметрии
В приведенном выше примере мы решили для t, применив свойство деления для создания эквивалентного уравнения. Иногда необходимо применить более одного такого свойства.
Пример 3 В уравнении ax + b = c найдите x через a, b и c.
Решение Мы можем решить для x, сначала добавив -b к каждому члену, чтобы получить
, затем разделив каждый член на a, мы получим
Обратные функции
Обратная функция — наоборот!
Начнем с примера:
Здесь у нас есть функция f (x) = 2x + 3 , записанная в виде блок-схемы:
Обратная функция идет другим путем:
Итак, обратное: 2x + 3: (y-3) / 2
Обратное значение обычно отображается путем добавления небольшого «-1» после имени функции, например:
ф -1 (г)
Мы говорим « f инверсия y»
Итак, обратное к f (x) = 2x + 3 записывается:
f -1 (y) = (y-3) / 2
(я также использовал y вместо x , чтобы показать, что мы используем другое значение.)
Вернуться туда, где мы начали
Самое замечательное в обратном преобразовании состоит в том, что он должен вернуть нам исходное значение:
.
Когда функция f превращает яблоко в банан,
Затем обратная функция f -1 превращает банан обратно в яблоко
Пример:
Используя приведенные выше формулы, мы можем начать с x = 4:
f (4) = 2 × 4 + 3 = 11
Затем мы можем использовать обратное для 11:
f -1 (11) = (11-3) / 2 = 4
И мы волшебным образом снова получаем 4 !
Мы можем написать это одной строкой:
f -1 (f (4)) = 4
«f, обратное f из 4, равно 4»
Таким образом, применение функции f, а затем ее обратной f -1 возвращает нам исходное значение снова:
f -1 (f (x)) = x
Мы могли бы также расположить функции в другом порядке, и он все еще работает:
f (f -1 (x)) = x
Пример:
Начать с:
f -1 (11) = (11-3) / 2 = 4
А потом:
f (4) = 2 × 4 + 3 = 11
Итак, мы можем сказать:
f (f -1 (11)) = 11
«f f, обратное 11, равно 11»
Решить с помощью алгебры
Мы можем вычислить обратное, используя алгебру. Положите y вместо f (x) и решите относительно x:
| Функция: | f (x) | = | 2x + 3 | |
| Положите «y» вместо «f (x)»: | y | = | 2x + 3 | |
| Вычтем 3 с обеих сторон: | г-3 | = | 2x | |
| Разделите обе стороны на 2: | (у-3) / 2 | = | х | |
| Стороны обмена: | x | = | (у-3) / 2 | |
| Решение (поместите «f -1 (y)» вместо «x»): | ф -1 (г) | = | (у-3) / 2 |
Этот метод хорошо подходит для более сложных инверсий.
Фаренгейта в Цельсия
Полезный пример — преобразование между градусами Фаренгейта и Цельсия:
Для преобразования Фаренгейта в Цельсия: f (F) = (F — 32) × 5 9
Обратная функция (Цельсия обратно к Фаренгейту): f -1 (C) = (C × 9 5 ) + 32
Для вас: посмотрите, сможете ли вы сделать шаги, чтобы создать инверсию!
Инверсия общих функций
До сих пор это было легко, потому что мы знаем, что обратное к умножению — это деление, а обратное к сложению — вычитание, но как насчет других функций?
Вот список, который вам поможет:
(Примечание: вы можете узнать больше об обратном синусе, косинусе и тангенсе.)
Осторожно!
Вы видели «Осторожно!» столбец выше? Это потому, что некоторые инверсии работают только с определенными значениями .
Пример: квадрат и квадратный корень
Когда мы возводим в квадрат отрицательное число , а затем делаем обратное, происходит следующее:
Квадрат: (- 2) 2 = 4
Обратная величина (квадратный корень): √ (4) = 2
Но мы не вернули исходное значение! Мы получили 2 вместо −2 .Наша вина в том, что мы не проявляем осторожности!
Таким образом, квадратная функция (как она есть) не имеет обратной
Но мы можем это исправить!
Ограничить домен (значения, которые могут входить в функцию).
Пример: (продолжение)
Только убедитесь, что мы не используем отрицательные числа.
Другими словами, ограничьте его до x ≥ 0 , и тогда мы сможем получить обратное.
Итак, мы имеем такую ситуацию:
- x 2 имеет ли не инверсию
- но {x 2 | x ≥ 0} (в котором говорится, что «x возведен в квадрат так, что x больше или равен нулю» с использованием нотации создателя множеств) имеет ли обратное.
Нет обратного?
Давайте посмотрим наглядно, что здесь происходит:
Чтобы иметь возможность иметь инверсию, нам нужно уникальных значений .
Подумайте … если есть два или более значений x для одного значения y , как мы узнаем, какое из них выбрать, когда вернемся?
| Общие функции |
| Без обратного |
Представьте, что мы перешли от x 1 к определенному значению y, куда мы вернемся? x 1 или x 2 ?
В этом случае у нас не может быть обратного.
Но если мы можем иметь ровно один x для каждого y, мы можем получить обратное.
Это называется «однозначным соответствием» или биективным, например
| Двухъективная функция |
| Имеет инверсию |
Функция должна быть «биективной», чтобы иметь инверсию.
Таким образом, биективная функция подчиняется более строгим правилам, чем общая функция, что позволяет нам иметь обратную функцию.
Домени диапазон
Так что же все эти разговоры о «, ограничивающем домен »?
В простейшей форме домен — это все значения, входящие в функцию (а диапазон , — это все значения, которые выходят).
В его нынешнем виде функция, приведенная выше, не имеет обратного значения , а не , потому что некоторые значения y будут иметь более одного значения x.
Но мы могли бы ограничить домен так, чтобы было уникальных x для каждого y …
… и теперь у нас может быть обратное:
Также примечание:
- Функция f (x) переходит из области в диапазон,
- Обратная функция f -1 (y) переходит из диапазона обратно в домен.
Давайте изобразим их оба в терминах x … так что теперь это f -1 (x) , а не f -1 (y) :
f (x) и f -1 (x) похожи на зеркальные изображения
(перевернут по диагонали).
Другими словами:
График f (x) и f -1 (x) симметричны по линии y = x
Пример: квадрат и квадратный корень (продолжение)
Первый , мы ограничиваем Домен до x ≥ 0 :
- {x 2 | x ≥ 0} «x в квадрате, так что x больше или равно нулю»
- {√x | x ≥ 0} «квадратный корень из x такой, что x больше или равен нулю»
И вы видите, что это «зеркальные отражения»
друг друга по диагонали y = x.
Примечание: когда мы ограничиваем область до x ≤ 0 (меньше или равно 0), обратное значение будет f -1 (x) = −√x :
- {x 2 | х ≤ 0}
- {−√x | x ≥ 0}
Которые тоже обратные.
Не всегда разрешимо!
Иногда невозможно найти обратную функцию.
Пример: f (x) = x / 2 + sin (x)
Мы не можем вычислить обратное, потому что мы не можем решить для «x»:
у = х / 2 + грех (х)
г …? = х
Примечания к обозначениям
Даже если мы пишем f -1 (x), «-1» — это , а не , показатель степени (или степени):
| f -1 (x) | … отличается от … | f (x) -1 |
| Функция, обратная функции f | f (x) -1 = 1 / f (x) (Обратный) |
Сводка
- Значение, обратное f (x), равно f -1 (y)
- Мы можем найти обратное, перевернув «блок-схему»
- Или мы можем найти обратное с помощью алгебры:
- Поместите «y» вместо «f (x)» и
- Решить относительно x
- Нам может потребоваться ограничить домен , чтобы функция имела инверсию
Как найти решение Набор
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.2 + 1 / х + 100]
Последнее обновление: 30 ноября 2019 г., Teachoo
Выписка
Пример 2 Найдите пределы: (i) (𝑙𝑖𝑚) ┬ (𝑥 → 1) [(𝑥2 + 1) / (𝑥 + 100)] (𝑙𝑖𝑚) ┬ (𝑥 → 1) [(𝑥2 + 1) / (𝑥 + 100)] Положив x = 1 = (12 + 1) / (1 + 100) = (1 + 1) / 101 = 𝟐 / 𝟏𝟎𝟏 Пример 2 Найдите пределы: (ii) (𝑙𝑖𝑚) ┬ (𝑥 → 2) [(𝑥 ^ 3 — 4𝑥 ^ 2 + 4𝑥) / (𝑥 ^ 2 — 4)] (𝑙𝑖𝑚) ┬ (𝑥 → 2) [(𝑥 ^ 3 — 4𝑥 ^ 2 + 4𝑥) / (𝑥 ^ 2 — 4)] = lim┬ (x → 2) 𝑥 (𝑥 ^ 2 — 4𝑥 + 4) / (𝑥 ^ 2 — 〖(2)〗 ^ 2) = lim┬ (x → 2) (𝑥 (𝑥 ^ 2 + 2 ^ 2 — 4𝑥)) / ((𝑥 — 2) (𝑥 + 2)) = lim┬ (x → 2) (𝑥 (𝑥 — 2) ^ 2) / ((𝑥 — 2) (𝑥 + 2)) = (𝒍𝒊𝒎) ┬ (𝒙 → 𝟐) 𝒙 (𝒙 — 𝟐) / (𝒙 + 𝟐) Положив x = 2 = (2 (2–2)) / (2 + 2) = (2 (0)) / 4 = 0/4 = 0 Пример 2 Найдите пределы: (iii) lim┬ (x → 2) [(x2 −4) / (x3 — 4×2 + 4x)] lim┬ (x → 2) [(x2 — 4) / (x3− 4×2 + 4x)] = lim┬ (x → 2) [(x2 — (2) 2) / (x (x2 — 4x + 4))] = lim┬ (x → 2) [((𝑥 — 2) (𝑥 + 2)) / (x (x (x — 2) — 2 (x — 2)))] = lim┬ (x → 2) [((𝑥 — 2) (𝑥 + 2)) / (𝑥 (x — 2) (x — 2))] = (𝐥𝐢𝐦) ┬ (𝐱 → 𝟐) [(𝒙 + 𝟐) / (𝐱 (𝐱 — 𝟐))] Положив x = 2 = (2 + 2) / (2 (2 — 2)) = (2 + 2) / (2 (2 — 2)) = 4 / (2 (0)) = 𝟒 / 𝟎 = ∞ Что не определено Пример 2 Найдите пределы: (iv) lim┬ (x → 2) [(x3 −2𝑥2) / (x2−5x + 6)] lim┬ (x → 2) [(x3 — 2𝑥2) / (x2 — 5x + 6)] = lim┬ (x → 2) ((x2 (x — 2)) / (𝑥2 — 3𝑥 — 2𝑥 + 6)) = lim┬ (x → 2) ((x2 (x — 2)) / (x (x — 3) — 2 (x — 3))) = lim┬ (x → 2) ((x2 (x — 2)) / ((x — 2) (x — 3))) = (𝐥𝐢𝐦) ┬ (𝐱 → 𝟐) ((𝐱𝟐) / ((𝐱 — 𝟑))) Положив x = 2 = (2) 2 / (2-3) = (2) 2 / (2-3) = 4 / (- 1) = — 4 Пример 2 Найдите пределы: (v) lim┬ (x → 1) [(x −2) / (x2 − x) — 1 / (𝑥3 −3𝑥2 + 2𝑥)] lim┬ (x → 1) [(x — 2) / (x2 — x) — 1 / (𝑥3 — 3𝑥2 + 2𝑥)] = lim┬ (x → 1) [(x — 2) / (x (x −1)) — 1 / (𝑥 (𝑥2 — 3𝑥 + 2))] = lim┬ (x → 1) [(x — 2) / (x (x −1)) — 1 / (𝑥 (𝑥2 — 2𝑥 — 𝑥 + 2))] = lim┬ (x → 1) [(x — 2) / (x (x −1)) — 1 / (𝑥 (𝑥 (𝑥 — 2) — 1 (𝑥 — 2)))] = lim┬ (x → 1) [(x — 2) / (x (x −1)) — 1 / (𝑥 (𝑥 — 1) (𝑥 — 2))] = lim┬ (x → 1) [((x — 2) (𝑥 — 2) — 1) / (𝑥 (𝑥 — 1) (𝑥 — 2))] = lim┬ (x → 1) [((x — 2) 2 — 1) / (𝑥 (𝑥 — 1) (𝑥 — 2))] = lim┬ (x → 1) [(𝑥2 + 2 ^ 2 — 4𝑥 — 1) / (𝑥 (𝑥 — 1) (𝑥 — 2))] = lim┬ (x → 1) [(𝑥2 + 4 — 4𝑥 — 1) / (𝑥 (𝑥 — 1) (𝑥 — 2))] = (𝐥𝐢𝐦) ┬ (𝒙 → 𝟏) [(𝒙𝟐 — 𝟒𝒙 — 𝟑) / (𝒙 (𝒙 — 𝟏) (𝒙 — 𝟐))] Положив x = 1 = (1 ^ 2 — 4 (1) + 3) / (1 (1 — 1) (1-2)) = 𝟎 / 𝟎 Поскольку это форма 0/0 мы можем упростить = lim┬ (x → 1) [(𝑥2 — 4𝑥 — 3) / (𝑥 (𝑥 — 1) (𝑥 — 2))] = lim┬ (x → 1) [(𝑥2 — 3𝑥 — 𝑥 + 3) / (𝑥 (𝑥 — 1) (𝑥 — 2))] = lim┬ (x → 1) [(𝑥 (𝑥 — 3) — 1 (𝑥 — 3)) / (𝑥 (𝑥 — 1) (𝑥 — 2))] = lim┬ (x → 1) [((𝑥 — 1) (𝑥 — 3)) / (𝑥 (𝑥 — 1) (𝑥 — 2))] = (𝐥𝐢𝐦) ┬ (𝒙 → 𝟏) [(𝒙 — 𝟑) / (𝒙 (𝒙 — 𝟐))] Положив x = 1 = (1-3) / (1 (1-2)) = (−2) / (1 × −1) = 2
Показать большеполиномов: объединение «похожих» терминов | Purplemath
Purplemath
Вероятно, наиболее распространенная вещь, которую вы будете делать с многочленами, — это «комбинировать одинаковые термины».Это процесс сложения любых терминов, которые вы можете, но не переусердствуйте, пытаясь сложить вместе термины, которые на самом деле не могут быть объединены. Итак, какие термины можно объединить с и почему?
Термины могут быть объединены только , если они имеют точно такую же переменную часть. И под «точно таким же» я подразумеваю «те же переменные, возведенные в одну и ту же степень». Вот краткое изложение того, что к чему:
MathHelp.com
Это , а не подобных терминов …
4 x и 3
… потому что первый член содержит переменную, а второй — нет.
Это , а не подобных терминов …
4 x и 3 y
… потому что два члена содержат разные переменные.
Это , а не подобных терминов …
4 x и 3 x 2
… потому что переменные одинаковы, а мощности этих переменных — нет.
Эти — это похожих терминов …
4 x и 3 x
… потому что переменные одинаковы, как и их мощность.
Но это не подобных терминов …
4 x и 3 xy
… потому что второй член имеет дополнительную переменную, поэтому части переменных не совпадают.
Итак, чтобы решить, являются ли два термина «подобными» терминами, которые можно объединить, мы смотрим на переменную часть этих терминов. Числовая часть двух терминов — это то, что будет объединено (как мы вскоре увидим), но именно переменная часть этих двух терминов определяет, могут ли термины объединяться. Чтобы их можно было комбинировать, части переменных терминов должны содержать одну и ту же переменную с одинаковой степенью (-ами).
После того, как вы определили, что два термина действительно являются «похожими» терминами и, следовательно, действительно могут быть объединены, вы можете работать с ними аналогично тому, как вы делали в гимназии.Когда вы только учились складывать, вы делали «пять яблок и шесть яблок — это одиннадцать яблок». С тех пор вы узнали, что, как говорится, «нельзя добавлять яблоки и апельсины». То есть «пять яблок и шесть апельсинов» — это просто большая груда фруктов; это не что-то вроде «одиннадцати аппланжей». Объединение одинаковых терминов работает примерно так же; мы добавляем числовые части, одновременно перемещая переменные части, почти как единицу или как добавленные нами «яблоки».
Глядя на эти два термина, я вижу, что каждый из них содержит переменную x , и переменная имеет одинаковую (понятную) степень 1 в каждом члене.Так что это похожие термины, и я могу их комбинировать.
Возвращаясь к арифметике в начальной школе, «три яблока плюс четыре яблока» были объединены в «семь яблок», если сложить три и четыре, чтобы получить семь, и взять с собой «яблоки» для поездки. Таким же образом я объединю эти два одинаковых термина, добавив числовую часть каждого члена, неся при себе x :
3 x + 4 x
(3 + 4) х
(7) x
Я показал каждый шаг выше, чтобы подчеркнуть, как сочетаются термины.Я складываю 3 и 4 и несу x вместе с числовым результатом. Мой ответ:
Упростить 2
x 2 + 3 x -4- x 2 + x + 9
Часто лучше сначала сгруппировать похожие термины, а затем упростить:
2 x 2 + 3 x — 4- x 2 + x + 9
(2 x 2 — x 2 ) + (3 x + x ) + (–4 + 9)
(2–1) x 2 + (3 + 1) x + (5)
(1) x 2 + (4) x + 5
x 2 + 4 x + 5
Во второй строке выше многие студенты считают полезным записывать понятный коэффициент 1 перед любыми выражениями переменных, не имеющих записанного коэффициента, как показано ниже красным:
(2 x 2 — x 2 ) + (3 x + x ) + (–4 + 9)
(2 x 2 — 1 x 2 ) + (3 x + 1 x ) + (–4 + 9)
(2–1) x 2 + (3 + 1) x + (5)
1 x 2 + 4 x + 5
x 2 + 4 x + 5
При упрощении таких выражений не требуется записывать «понятый 1», но многие студенты находят этот метод очень полезным, по крайней мере, когда они только начинают.Какой метод поможет вам последовательно правильно завершить упрощение, это тот метод, который вы должны использовать.
Упростить 10
x 3 -14 x 2 + 3 x -4 x 3 + 4 x -6
Я начну с группировки терминов по степени.
10 x 3 -14 x 2 + 3 x -4 x 3 + 4 x -6
(10 x 3 — 4 x 3 ) + (–14 x 2 ) + (3 x + 4 x ) — 6
6 x 3 -14 x 2 + 7 x -6
Предупреждение: при перемещении терминов помните, что знаки терминов перемещаются на вместе с ними.Не портите себя, оставляя позади осиротевшие знаки «плюс» и «минус».
Если это поможет вам разобраться, перепишите выражение следующим образом:
10 x 3 + (–14 x 2 ) + 3 x + (–4 x 3 ) + 4 x + (–6)
Превращая вычитания в сложения отрицаний, становится ясно, где принадлежат знаки «минус», и их легче перемещать правильно:
10 x 3 + (–4 x 3 ) + (–14 x 2 ) + 3 x + 4 x + (–6)
(10-4) x 3 -14 x 2 + (3 + 4) x -6
…и так далее. Делайте то, что работает для вас.
Упростить 25 — (
x + 3- x 2 )
Первое, что мне нужно сделать, это взять отрицательный результат в круглые скобки:
25 — ( x + 3- x 2 )
25-90 619 x -3 + x 2
Хорошо; эти термины не только не в порядке убывания, они почти полностью перевернуты! Я поставлю их в правильном направлении, а затем упрощу, объединив две константы, которые являются единственными подобными терминами:
x 2 — x + 25-3
x 2 — x + 22
Многие студенты, особенно в начале обучения, испытывают трудности со знаком «минус», в том числе при вводе их в скобки, как я только что сделал выше.Если это помогает вам отслеживать, что происходит, попробуйте поставить «понято» 1 перед круглыми скобками (выделено красным ниже), а затем перейти к терминам внутри:
25 — ( x + 3- x 2 )
25-1 ( x + 3- x 2 )
25 — 1 ( x ) — 1 (+3) — 1 (- x 2 )
25 — 1 x — 3 + 1 x 2
1 x 2 — 1 x + 25 — 3
1 x 2 — 1 x + 22
x 2 — x + 22
В то время как первый формат (без записи 1) является более «стандартным» форматом, математически допустимы оба формата.Вам следует использовать тот формат, который вам больше всего подходит. Не стесняйтесь вставлять понятную 1, когда начинаете; не чувствуйте себя обязанным продолжать использовать его, как только вы почувствуете себя уверенно без него.
Упростить
x + 2 ( x — [3 x — 8] + 3)
Это просто проблема порядка операций с переменной в ней.Если я работаю аккуратно изнутри, обращая особое внимание на свои знаки «минус», то со мной все будет в порядке:
x + 2 ( x — [3 x — 8] + 3)
x + 2 ( x — 1 [3 x — 8] + 3)
x + 2 ( x — 1 [3 x ] — 1 [–8] + 3)
x + 2 ( x -3 x + 8 + 3)
x + 2 (–2 x + 11)
x + 2 (–2 x ) + 2 (+11)
x -4 x + 22
1 x -4 x + 22
–3 x + 22
Просто чтобы вы знали, это та проблема, которую мы, учителя математики, любим, ставим на тесты (да, некоторые из нас вроде как больные щенки), поэтому вы должны ожидать, что вам понадобится иметь дело с вложенными символами группировки так.
Упростить [(6
x — 8) — 2 x ] — [(12 x — 7) — (4 x — 5)]
Работаю изнутри:
[(6 x — 8) — 2 x ] — [(12 x — 7) — (4 x — 5)]
[6 x — 8 — 2 x ] — [12 x — 7 — 1 (4 x ) — 1 (–5)]
[6 x — 2 x — 8] — [12 x — 7 — 4 x + 5]
[4 x — 8] — [12 x — 4 x — 7 + 5]
4 x — 8 — [8 x -2]
4 x — 8 — 1 [8 x ] — 1 [–2]
4 x -8-8 x + 2
4 x — 8 x — 8 + 2
–4 x — 6
Упростить –4
y — [3 x + (3 y — 2 x + {2 y — 7}) — 4 x + 5]
Как всегда, я начну с самой внутренней группировки и упрощу свой путь к ответу.
–4 y — [3 x + (3 y — 2 x + {2 y — 7}) — 4 x + 5]
–4 y — [3 x + (3 y — 2 x + 2 y — 7) — 4 x + 5]
–4 y — [3 x + (–2 x + 3 y + 2 y — 7) — 4 x + 5]
–4 y — [3 x + (–2 x + 5 y — 7) — 4 x + 5]
–4 y — [3 x — 2 x + 5 y — 7 — 4 x + 5]
–4 y — [3 x — 2 x — 4 x + 5 y — 7 + 5]
–4 y — [3 x — 6 x + 5 y — 7 + 5]
–4 y — [–3 x + 5 y — 2]
–4 y — 1 [–3 x ] — 1 [+5 y ] — 1 [–2]
–4 y + 3 x — 5 y + 2
3 x -4 y -5 y + 2
3 x -9 y + 2
В приведенном выше упрощении участвовали две разные переменные.Принято (хотя и не требуется) перечислять термины так, чтобы их переменные располагались в алфавитном порядке. Вот почему я перечислил 3 x перед 9 y . Как всегда, в самом конце идет постоянный член.
(Если вы считаете, что вам нужно больше практики с этим последним типом задач (со всеми скобками, минусами и круглыми скобками, тогда вы можете просмотреть урок «Упрощение с круглыми скобками»).
Когда мы говорим о яблоках и апельсинах, обычно довольно легко понять, что следует сочетать с чем еще и каким образом.Но как только мы начнем работать с переменными, все может запутаться. Не заблуждайтесь и не путайте умножение и сложение. Для меня это может показаться глупым, но это может быть наиболее частая ошибка студентов при объединении одинаковых терминов (после нарушения порядка операций).
Это умножение …
( x ) ( x ) = ( x 1 ) ( x 1 )
= x 1 + 1 = x 2
… так что это упрощается с помощью правил комбинирования экспонент.
Это дополнение …
x + x = 1 x + 1 x
= (1 + 1) x = 2 x
… так что это упрощается с помощью правил комбинирования коэффициентов.
Позвольте мне внести ясность:
( x ) ( x ) не равно x + x
x 2 не равно 2 x
Итак, если у вас есть что-то вроде x 3 + x 2 , не пытайтесь сказать, что это как-то равно примерно x 5 или 5 x .Термины не похожи друг на друга и не могут быть объединены. Если у вас есть что-то вроде 2 x + x , не пытайтесь сказать, что это как-то равно 2 x 2 . Эти термины похожи на термины и объединяются путем сложения их коэффициентов.
Не торопитесь и убедитесь, что вы постоянно держите в голове, как работает умножение, а не как работает сложение. Фактически, «комбинирование похожих терминов» — это тема, для которой было бы трудно выполнить слишком много практики .Выполняйте как можно больше практических задач!
URL: https://www.purplemath.com/modules/polydefs2.htm
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в объединении «похожих» терминов. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку и выберите «Объединить» или «Упростить», чтобы сравнить свой ответ с ответом Mathway.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
Три правила экспонент — Полный курс алгебры
Урок 13, Раздел 2
Вернуться в раздел 1
Правило 1. То же основание
Правило 2.Мощность изделия
Правило 3. Мощность мощности
Правило 1. То же основание
«Чтобы умножить степени одного основания, сложите экспоненты».
Например, a 2 a 3 = a 5 .
Почему мы складываем экспоненты? Из-за того, что означают символы. Раздел 1.
Пример 1.Умножение 3 x 2 · 4 x 5 · 2 x
Решение . Задача означает (Урок 5): умножьте числа, затем сложите степени x :
.3 x 2 · 4 x 5 · 2 x = 24 x 8
Два фактора x — x 2 — умножить на пять факторов x — x 5 — умножить на один фактор x , произвести всего 2 + 5 + 1 = 8 множителей x : x 8 .
Задача 1. Умножить. Примените правило Same Base.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
| а) | 5 x 2 · 6 x 4 = 30 x 6 | б) | 7 x 3 · 8 x 6 = 56 x 9 | ||||
| в) | x · 5 x 4 = 5 x 5 | г) | 2 x · 3 x · 4 x = 24 x 3 | ||||
| e) | x 3 · 3 x 2 · 5 x = 15 x 6 | е) | x 5 · 6 x 8 y 2 = 6 x 13 y 2 | ||||
| г) | 4 x · y · 5 x 2 · y 3 = 20 x 3 y 4 | ч) | 2 x y · 9 x 3 y 5 = 18 x 4 y 6 | ||||
| i) | a 2 b 3 a 3 b 4 = a 5 b 7 | к) | a 2 bc 3 b 2 ac = a 3 b 3 c 4 | ||||
| к) | x m y n x p y q = x 9039 n + q | л) | a p b q ab = a p + 1 b q + 1 | ||||
Проблема 2.Различают следующие:
x · x и x + x .
x · x = x ². x + x = 2 x .
Пример 2. Сравните следующее:
а) x · x 5 б) 2 · 2 5
Решение .
a) x · x 5 = x 6
b) 2 · 2 5 = 2 6
Часть b) имеет ту же форму , что и часть a). Это часть а) с x = 2.
Один множитель 2 умножает пять множителей 2, получая шесть множителей 2.
2 · 2 = 4 здесь неверно.
Проблема 3. Примените правило Same Base.
| а) | x x 7 = x 8 | б) | 3 · 3 7 = 3 8 | в) | 2 · 2 4 · 2 5 = 2 10 | ||
| г) | 10 · 10 5 = 10 6 | д) | 3 x · 3 6 x 6 = 3 7 x 7 | ||||
Проблема 4.Примените правило Same Base.
| а) | x n x 2 = x n + 2 | б) | x n x = x n + 1 | ||||
| в) | x n x n = x 2 n | г) | x n x 1- n = x | ||||
| e) | x · 2 x n — 1 = 2 x n | е) | x n x m = x n + m | ||||
| г) | x 2 n x 2- n = x n + 2 | ||||||
Правило 2: Сила произведения факторов
«Увеличьте каждый коэффициент до той же степени.«
Например, ( ab ) 3 = a 3 b 3 .
Почему мы можем это сделать? Опять же, в соответствии с тем, что означают символы:
( ab ) 3 = ab · ab · ab = aaabbb = a 3 b 3 .
Порядок факторов не имеет значения:
ab · ab · ab = aaabbb .
Задача 5. Применить правила экспонент.
| а) | ( x y ) 4 = x 4 y 4 | б) | ( pqr ) 5 = p 5 q 5 r 5 | в) | (2 abc ) 3 = 2 3 a 3 b 3 c 3 |
| d) x 3 y 2 z 4 ( xyz ) 5 | = | x 3 y 2 z 4 · x 5 y 5 z 5 Правило 2. |
| = | x 8 y 7 z 9 То же основание. | |
Правило 3: Степень мощности
«Чтобы взять степень степени, умножьте экспонент».
Например, ( a 2 ) 3 = a 2 · 3 = a 6 .
Почему мы это делаем? Опять же, из-за того, что означают символы:
( a 2 ) 3 = a 2 a 2 a 2 = a 3 ·0 2
=
Задача 6. Примените правила экспонент.
| а) | ( x 2 ) 5 = x 10 | б) | ( a 4 ) 8 = a 32 | в) | (10 7 ) 9 = 10 63 |
Пример 3.Примените правила экспонент: (2 x 3 y 4 ) 5
Решение . В скобках указаны три фактора: 2, x 3 и y 4 . Согласно Правилу 2 мы должны взять пятую степень каждого из них. Но чтобы взять степень степени, мы умножаем показатели. Следовательно,
(2 x 3 y 4 ) 5 = 2 5 x 15 y 20
Проблема 7.Применяйте правила экспонент.
| а) | (10 a 3 ) 4 = 10 000 a 12 | б) | (3 x 6 ) 2 = 9 x 12 | |
| в) | (2 a 2 b 3 ) 5 = 32 a 10 b 15 | г) | ( xy 3 z 5 ) 2 = x 2 y 6 z 10 | |
| e) | (5 x 2 y 4 ) 3 = 125 x 6 y 12 | е) | (2 a 4 bc 8 ) 6 = 64 a 24 b 6 c 48 | |
Проблема 8.Применяйте правила экспонент.
a) 2 x 5 y 4 (2 x 3 y 6 ) 5 = 2 x 5 y 7 2 5 x 15 y 30 = 2 6 x 20 y 34
b) abc 9 ( a 2 b 3 c 4 ) 8 = abc 9 · a 16 b 24 c 32 = a 17 b 25 c
Проблема 9.Используйте правила экспонент, чтобы вычислить следующее.
а) (2 · 10) 4 = 2 4 · 10 4 = 16 · 10 000 = 160 000
б) (4 · 10 2 ) 3 = 4 3 · 10 6 = 64 000 000
в) (9 · 10 4 ) 2 = 81 · 10 8 = 8,100,000,000
В степенях 10 столько же нулей, сколько в экспоненте 10.
Пример 4. Квадрат x 4 .
Решение . ( x 4 ) 2 = x 8 .
Чтобы возвести в квадрат степень, удвойте показатель степени.
Проблема 10. Возведите следующее.
| а) | x 5 = x 10 | б) | 8 a 3 b 6 = 64 a 6 b 12 | |
| в) | −6 x 7 = 36 x 14 | г) | x n = x 2 n | |
Часть c) иллюстрации: Квадрат числа никогда не бывает отрицательным.
(−6) (- 6) = +36. Правило знаков.
Задача 11. Примените правило экспонент — если возможно.
| а) | x 2 x 5 = x 7 , Правило 1. | б) | ( x 2 ) 5 = x 10 , Правило 3. |
| в) | x 2 + x 5 |
| Невозможно. Правила экспонент применяют только к умножению. |
В итоге: Добавьте показателей степени, когда одно и то же основание появляется дважды: x 2 x 4 = x 6 . Умножьте экспоненты, когда основание появится один раз — и в скобках: ( x 2 ) 5 = x 10 .
Задача 12. Примените правила экспонент.
| а) | ( x n ) n = x n · n = x n | б) | ( x n ) 2 = x 2 n | |
Проблема 13.Примените правило экспонент или добавьте похожие термины — если возможно.
а) 2 x 2 + 3 x 4 Невозможно. Это не похоже на термины .
б) 2 x 2 · 3 x 4 = 6 x 6 . Правило 1.
в) 2 x 3 + 3 x 3 = 5 x 3 .Как термины. Показатель степени не меняется.
г) x 2 + y 2 Невозможно. Это не похоже на термины.
e) x 2 + x 2 = 2 x 2 . Как термины.
е) x 2 · x 2 = x 4 . Правило 1
г) x 2 · y 3 Невозможно.Разные базы.
ч) 2 · 2 6 = 2 7 . Правило 1
i) 3 5 + 3 5 + 3 5 = 3 · 3 5 (при добавлении подобных терминов) = 3 6 .
Мы продолжим правила экспонентов в 21 уроке.
Следующий урок: Умножение. Распределительное правило.
Вернуться в раздел 1
Содержание | Дом
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
Уравнения абсолютных значений
Уравнения абсолютных значений Уравнения абсолютных значенийВыполните следующие действия, чтобы найти равенство по абсолютной величине. который содержит одно абсолютное значение:
- Выделите абсолютное значение на одной стороне уравнения.
- Число на другой стороне уравнения отрицательное? Если вы ответили утвердительно, то уравнение не имеет решения. Если вы ответили нет, переходите к шагу 3.
- Напишите два уравнения без абсолютных значений. Первое уравнение установит количество внутри столбцов, равное количеству на другом сторона знака равенства; второе уравнение установит количество внутри столбцы равны противоположному числу на другой стороне.
- Решите два уравнения.
Выполните следующие действия, чтобы найти равенство абсолютного значения.
который содержит два абсолютных значения (по одному с каждой стороны уравнения):
- Напишите два уравнения без абсолютных значений.Первый уравнение установит количество внутри столбцов с левой стороны равным количество внутри полос с правой стороны. Второе уравнение установит количество внутри столбцов с левой стороны равным противоположному количества внутри полос с правой стороны.
- Решите два уравнения.
Давайте рассмотрим несколько примеров.
Пример 1: Решить | 2x — 1 | + 3 = 6
| Шаг 1: Изолировать абсолютное значение | | 2x — 1 | + 3 = 6 | 2x — 1 | = 3 | |
| Шаг 2: Is число на другой стороне уравнения отрицательное? | Нет, это положительное число, 3, так что продолжайте шаг 3 | |
| Шаг 3: Запись два уравнения без столбцов абсолютных значений | 2x — 1 = 3 | 2х — 1 = -3 |
| Шаг 4: Решить оба уравнения | 2x — 1 = 3 2x = 4 х = 2 | 2х — 1 = -3 2x = -2 х = -1 |
Пример 2: Решить | 3x — 6 | — 9 = -3
| Шаг 1: Изолировать абсолютное значение | | 3х — 6 | — 9 = -3 | 3x — 6 | = 6 | |
| Шаг 2: Is число на другой стороне уравнения отрицательное? | Нет, это положительное число, 6, так что продолжайте шаг 3 | |
| Шаг 3: Запись два уравнения без столбцов абсолютных значений | 3х — 6 = 6 | 3х — 6 = -6 |
| Шаг 4: Решить оба уравнения | 3х — 6 = 6 3x = 12 х = 4 | 3х — 6 = -6 3x = 0 х = 0 |
Пример 3: Решить | 5x + 4 | + 10 = 2
| Шаг 1: Изолировать абсолютное значение | | 5x + 4 | + 10 = 2 | 5x + 4 | = -8 |
| Шаг 2: Is число на другой стороне уравнения отрицательное? | Да, это отрицательное число, -8.Нет решения к этой проблеме. |
Пример 4: Решить | x — 7 | = | 2x — 2 |
| Шаг 1: Запись два уравнения без столбцов абсолютных значений | х — 7 = 2х — 2 | х — 7 = — (2х — 2) |
| Шаг 4: Решить оба уравнения | х — 7 = 2х — 2 -x — 7 = -2 -x = 5 х = -5 | х — 7 = -2x + 2 3x — 7 = 2 3x = 9 х = 3 |
Пример 5: Решить | x — 3 | = | x + 2 |
| Шаг 1: Запись два уравнения без столбцов абсолютных значений | х — 3 = х + 2 | х — 3 = — (х + 2) |
| Шаг 4: Решить оба уравнения | х — 3 = х + 2 — 3 = -2 ложное заявление Нет решения из этого уравнения | х — 3 = -x — 2 2x — 3 = -2 2x = 1 х = 1/2 |
Итак, единственное решение этой проблемы — x = 1/2
Пример 6: Решить | x — 3 | = | 3 — x |
| Шаг 1: Запись два уравнения без столбцов абсолютных значений | х — 3 = 3 — х | х — 3 = — (3 — х) |
| Шаг 4: Решить оба уравнения | х — 3 = 3 — х 2x — 3 = 3 2x = 6 х = 3 | х — 3 = — (3 — х) х — 3 = -3 + х -3 = -3 Все действительные числа являются решениями этого уравнения |
Так как 3 входит в набор действительных чисел, мы просто скажем, что решение этого уравнения — все действительные числа.
 Если цены по контракту фиксированные, то в столбце проставляются прочерки.
Если цены по контракту фиксированные, то в столбце проставляются прочерки. Консоли кабельные КС1, КС2, КС3 также крепятся на стойки кабельные СТ с помощью болтовых соединений.
Консоли кабельные КС1, КС2, КС3 также крепятся на стойки кабельные СТ с помощью болтовых соединений. Консоль КС2 больше подходит для установки на стойки СТ.
Консоль КС2 больше подходит для установки на стойки СТ.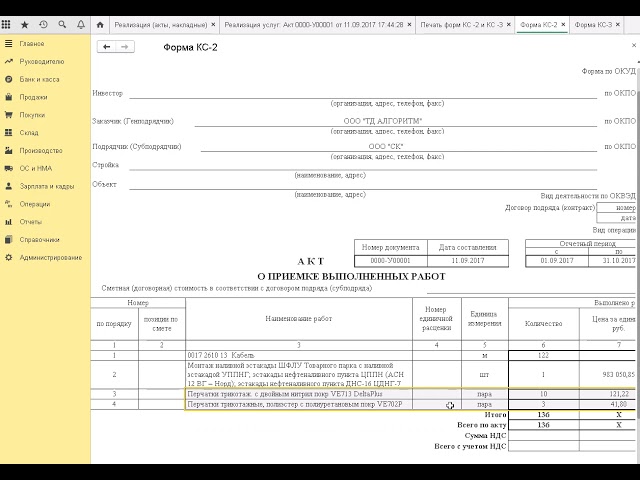 Вес изделия соответственно изменится.
Вес изделия соответственно изменится.