Что такое сложные проценты по вкладу: стоит ли открывать вклады с плавающей ставкой :: Финансы :: РБК

Сложные проценты на примерах

Задачи на сложные проценты решаются в достаточно быстрый способ при знании нескольких простых формул. Часть из них касается начислений по вкладу или кредиту, когда те осуществляются через определенные промежутки времени . Также сложные проценты используют в задачах химии, медицины и ряде других сфер.

ФОРМУЛЫ СЛОЖНЫХ ПРОЦЕНТОВ

В случае размещения вкладов с капитализацией процентов на годы конечная сумма депозита определяется формулой
Здесь P – первоначальный взнос, r – процентная ставка, n – количество лет. По сложным процентам работают банки, инвестиционные фонды, страховые компании. Распространенные за рубежом, а теперь и в Украине — пенсионные фонды и фонды страхования жизни работают по схеме сложных процентов.
При размещении вкладов с капитализацией процентов ежеквартально формула сложных процентов будет выглядеть
где q – количество полных кварталов.
При капитализации процентов ежемесячно применяют следующую формулу для вычислений
где s – количество месяцев существования соглашения.
Последний случай, непрерывное начисление процентов, когда сложные проценты начисляются ежедневно, рассчитывают по формуле
где m – количество дней.
Страхование жизни и откладывания пенсий исчисляют сложными формулами, кроме начисления сложных процентов ежегодно осуществляются необходимые взносы.
Рассмотрим два случая накопления. Мужчина откладывает 5000 грн. в течение 20 лет. За это время он отложит
20*5000=100000 (грн).
При откладывании в накопительные фонды с годовой ставкой 13%, за первый год сумма возрастет до
5000*(1+13/100)=5650 (грн).
В следующем году человек в данной суммы добавляет еще 5000 грн. В результате, за второй год сумма увеличится
(5650+5000)*(1+0,13)=12034.50 (грн) .
Продолжая подобные вычисления, в конце срока получим сумму размером 457349,58 грн.
Поверьте — ошибок при исчислении форуме, большое значение набегает за счет сложных процентов. Сомнительным остается только история изменения платежеспособности гривны через 20 лет. Учитывая политику государства вкладывать деньги в такие фонды люди не спешат, однако за рубежом практика откладывания денег распространена, правда процентные ставки намного ниже.

Рассмотрим распространенные задачи на сложные проценты.

Пример 1. Вкладчик положил на депозит $ 3000 под 9% годовых на 10 лет. Какая сумма аккумулируется конце 10-го года при годовой капитализации? На сколько вырастет сумма по сравнению с первоначальным взносом?

Решение: Применяем формулу сложных процентов для нахождения суммы в конце срока

Чтобы ответить на второй вопрос, от значения 7102,09 вычитаем сумму вклада.

Разница составляет 4102 доллара.

 

Пример 2. Инвестор вложил 7000 грн под 10% годовых при условии начисления сложных процентов ежеквартально. Какую сумму он получит через 8 лет?

Решение: Применяем 2 формулу сложных процентов. Находим количество кварталов
8*4=32.
и подставляем в формулу

Школьные задачи на сложные проценты

Например, возьмем задачи из учебника для 9 класса авторов А. Г. Мерзляк, В.Б. Полонский, М.С. Якир «Аглгебра». (Номер в скобках)

Задача 1. (556) Костюм стоил 600 грн. После того как цена была снижена дважды, он стал стоить 432 грн., Причем процент снижения второй был в 2 раза больше, чем в первый раз. На сколько процентов каждый раз снижалась цена?

Решение: Для упрощения вычислений обозначим
X – первая скидка;
X/2 – вторая скидка.
Для вычисления неизвестной X составляем уравнение

Упрощаем, и сводим к квадратному уравнению

и решаем


Первый решение не имеет физического смысла, второй учитываем при вычислениях. Значение 0,2 соответствует снижению на 0,2*100%=20% после первой скидки, и X/2 =10% после второй скидки.

 

Задача 2. (557) Определенный товар стоил 200 грн. Сначала его цену повысили на несколько процентов, а затем снизили на столько же процентов, после чего стоимость его стала 192 грн. На сколько процентов каждый раз происходила смена цены товара?

Решение: Поскольку проценты одинаковы, то обозначаем изменении цены товара через X.
На основе условия задачи получим уравнение

Его упрощение приведет к решению уравнения

откуда корни приобретут значений

Первая значение отвергаем, оно меняет суть задачи (сначала имеем снижение, а затем рост процентов, противоречит условию). Второе при пересчете составит 0,2*100%=20% процентов.

 

Задача 3. (558) Вкладчик положил в банк 4000 грн. За первый год ему начислена определенный процент годовых, а второго года банковский процент увеличен на 4%. На конец второго года на счете стало 4664 грн. Сколько процентов составила банковская ставка в первый год?

Решение: Обозначим через X – увеличение вклада в первый год, тогда
X+4/100%=X+0,04
начисления во второй год.
По условию задачи составляем уравнение для определения неизвестной X

После упрощений получим квадратное уравнение вида

Вычисляем дискриминант

и корни уравнения

Первый корень отбрасываем, второй соответствует ставке в 6% годовых.

 

Задача 4. (564) В сосуде 12 кг кислоты. Часть кислоты отлили и долили до прежнего уровня водой. Затем снова отлили столько же, как и в первый раз, и долили водой до прежнего уровня. Сколько литров жидкости отливали каждый раз, если в результате получили 25-процентный раствор кислоты?

Решение: Обозначим через X – часть кислоты, которую отливали.
После первого раза ее осталось 12-X, а процентное содержание кислоты

После второй попытки содержание кислоты в сосуде составило
.
Разведя водой до 12 кг, процентное содержание составляло 25%. Составляем уравнение

Упрощаем проценты и избавляемся знаменателей


Решаем квадратное уравнение


Условии задачи удовлетворяет второе решение, а это значит, что каждый раз отливали 6 кг жидкости.

На этом знакомство со сложными процентами завершается. На практике Вам встретятся как простые так и сложные задачи. При проблемах с вычисления сложных процентов обращайтесь к нам, мы поможем Вам в решении задач.

Калькулятор вклада с капитализацией, пополнением, частичным снятием, пролонгацией

Преимущества калькулятора вкладов Fin-Plus.ru

Калькулятор вкладов с капитализацией

В договоре каждого банковского вклада прописывается один из двух возможных способов учета начисляемых процентов: с капитализацией или без нее. Если предусмотрена капитализация, то регулярно начисляемые проценты прибавляются к основной сумме вклада, и каждое последующее начисление будет происходить уже на на большую сумму (так называемый сложный процент). В режиме без капитализации процентов, весь начисляемый доход перечисляется на отдельный банковский счет, и в последующем начислении процентов не участвует. При одинаковых процентных ставках и прочих равных условиях вклады с капитализацией являются более предпочтительными, так как они принесут вкладчику больший доход. Причем, чем чаще будет происходить капитализация, тем выше будет итоговый доход.

Для выбора нужного режима установите или снимите галочку «с капитализацией» в графе «Начисление процентов»

Калькулятор вкладов с пополнениями и частичными снятиями

Если в вашем депозитном договоре была прописана возможность пополнения, и вы ею воспользовались в течение срока вклада, то в графе калькулятора «Пополнения вклада» необходимо добавить столько строк, сколько пополнений было сделано вами. В каждой строке нужно указать сумму и дату пополнения.

Аналогично в графе «Частичные снятия» указываются данные о снятиях, которые вы совершили. В случае частичных снятий с депозита, на котором не происходит капитализация процентов (а происходит начисление процентов на отдельный, например, текущий счет) нужно выбрать с какого именно счета снимаются деньги. Если в депозитном договоре прописана сумма неснижаемого остатка, то при ее указании в калькуляторе будет происходить дополнительная проверка на то, что очередное снятие не приведет к чрезмерному уменьшению остатка на счете.

Плавающая и фиксированная процентная ставка

Если в депозитном договоре установлено, что в течении всего срока проценты будут начисляться по фиксированной ставке, или отсутствует упоминание об условиях изменения величины ставки, то в графе калькулятора «Процентная ставка» следует указать, что ставка является фиксированной и ввести ее значение. Этот вариант является наиболее распространенным (более 95% всех вкладов, рассчитанных на Fin-Plus. ru).

В случае, когда ставка является плавающей в зависимости от суммы на депозитном счете, в калькулятор необходимо ввести несколько строк, каждая их которых определяет нижний предел (минимальную сумму), начиная с которой будет действовать введенное значение ставки. Верхний предел (максимальная сумма, до которой действует введенная ставка) будет определяться следующим в порядке возрастания суммы значением, т.е. последующей введенной строкой.

Еще один возможный вариант, предлагаемый некоторыми банками, определяет, что ставка начисления процентов будет

плавающей в зависимости от срока, в течение которого ваши деньги находятся в банке. В этом случае в калькуляторе, выбрав соответствующий вид ставки, нужно ввести несколько строк, по одной для каждого значения ставки. Каждая строка определяет временной интервал действия ставки. День (от начала срока вклада) окончания такого интервала (более поздний срок) вводится явно, а в качестве дня начала интервала (более ранняя дата) калькулятор использует или день вклада или день, следующий за указанным в качестве дня окончания предыдущего интервала. Например, если в договоре вклада продолжительностью 1 год прописано, что с первого по сотый день вклада действует ставка 10%, а со сто первого дня и до конца срока действует ставка 12%, то в калькулятор следует ввести две строки со следующими значениями: 1) Номер дня = 100, Ставка = 10%; 2) Номер дня = 366, Ставка = 12%

Налог на вклад

В Налоговом Кодексе РФ прописано, что когда процентная ставка по вкладу физического лица превышает определенный предел (9% для валютных вкладов, значение ставки рефинансирования ЦБ + 5% для вкладов в рублях), то с суммы этого превышения удерживается налог (30% или 35%) в пользу государства. И банк в этом случае будет выступать как налоговый агент, т.е. перечислять деньги в казну независимо от воли вкладчика. Это приводит к уменьшению суммы, которую вкладчик получит по окончании срока депозита. Более подробно порядок удержания налога рассмотрен в отдельной статье. Для корректного определения величины налоговой ставки в калькуляторе важно правильно установить галочку в графе «Местожительство». Если вы проводите в России менее половины года, то вы можете претендовать на пониженную налоговую ставку 30%, и в этом случае галочку нужно снять. Но будьте готовы к тому, что банк запросит у вас подтверждающие документы.

Пролонгация вклада

Если ваш договор банковского вклада предусматривает автоматическое продление на условиях, действовавших на день вклада, то в графе «Пролонгация вклада» укажите, сколько раз вы воспользовались этой возможностью. Если же условия депозита (например, величина ставки) изменяются каждый раз на день пролонгации, то для расчета в калькуляторе итоговой суммы нужно последовательно рассчитать исходный и пролонгированные депозиты, каждый раз вводя новую сумму и дату вклада (их можно взять из результатов предыдущего расчета), а также ставку вклада (ее можно посмотреть в договоре или на сайте банка).

Способы начисления процентов

Калькулятор вкладов поддерживает все используемые банками способы начисления процентов. Как более распространенные: ежегодное, ежеквартальное, ежемесячное начисление процентов.

Так и относительно редкие: полугодовое, еженедельное или ежедневное начисление процентов. Способ начисления через заданный интервал подходит для случая, когда банк регулярно перечисляет проценты через равные промежутки времени, например каждые 12 дней.

Перенос дней начисления процентов

Большинство банков производят начисление процентов независимо от того, является ли очередная дата начисления рабочим днем или выходным. Другие банки проводят все операции только по рабочим дням в соответствии с производственным календарем. И когда дата начисления или капитализации процентов согласно договору выпадает на нерабочий, то банк осуществляет перенос на ближайший предшествующий или последующий рабочий день. Вследствие такого переноса изменяется не дата операции, но и сумма начисленного процентного дохода. В графе «Учет выходных дней и праздников» выберите нужные настройки на основе данных вашего депозитного договора.

Сохранение расчета вклада и выгрузка в Excel

После того как ваш вклад рассчитан, вы можете выгрузить все результаты в Excel и распечатать их. Каждый расчет получает свой уникальный код (deposit_id), по которому вы впоследствии можете вновь вернуться к нему и внести изменения при необходимости

Расчет эффективной процентной ставки и доходности

Ставка, указанная в договоре банковского вклада, является номинальной. Она является основным, но не единственным фактором, определяющим фактическую сумму полученного дохода. Двумя другими оказывающими влияниями факторами являются частота (периодичность) капитализации начисленных процентов и налог, удерживаемый при начислении этих процентов. При одинаковой номинальной ставке вклад с ежемесячной капитализацией окажется доходнее, чем вклад с ежегодной капитализацией. Рассчитав все суммы и даты начисленного процентного дохода, калькулятор вычисляет и эффективную процентную ставку по вкладу

, которая определяет, насколько быстро приумножались бы ваши деньги в эталонных условиях, когда капитализация происходит один раз в год, а налог отсутствует. Именно по величине эффективной ставки имеет смысл сравнивать различные вклады между собой. Она является как бы «единым знаменателем», показывающим эффективность работы денег на вкладах с разными условиями.

Для вкладов, по которым не было ни пополнений, ни снятий, калькулятор также рассчитывает величину доходности вкладов, которая равна отношению чистого полученного дохода к сумме вклада, но которая в отличие от эффективной ставки не учитывает срок, за который был получен доход.

Проценты по вкладу и инфляция

В условиях, когда происходит постоянный рост цен на товары и услуги, при расчете прибыльности того или иного вложения необходимо учитывать темпы инфляции. Иначе может возникнуть ситуация, когда рассчитанная инвестиция кажется прибыльной (значение эффективной процентой ставки больше 0), а по факту инфляция «съедает» не только процентный доход, но и основной капитал, т.е. уменьшается покупательная способность суммы на депозите.

Если срок вклада уже завершился, то калькулятор рассчитает среднегодовую инфляцию в России за период вклада. Если вклад все еще открыт или будет открыт в будущем (т.е. дата окончания вклада больше, чем дата расчета), то калькулятор посчитает индекс российской инфляции за последний год. За такой же период будут рассчитаны проценты изменения курса евро и и курса доллара. Сравнение эффективной процентой ставки с этими показателями позволит сформировать более полное представление о выгодности вклада.

Калькулятор вкладов в валюте

С помощью калькулятора можно рассчитать вклады не только в рублях, но и в нескольких популярных валютах (евро, доллары, британские фунты, украинские гривны, китайские юани и др.). При этом сумма удержанного налога будет автоматически пересчитана в рубли по курсу ЦБ РФ, действующему на дату перечисления или капитализации процентного дохода.

Точный расчет

Полный расчет с точностью «до копейки» процентного дохода, налога на вклад, доходности, эффективной процентной ставки, дат и сумм выплат по вкладу становится возможным благодаря поддержке в калькуляторе всех вышеперечисленных особенностей. У вкладчика появляется независимый инструмент проверки своих расчетов с банком. О других способах проверки написано в этой статье.

Если вы выявили расхождение между выполненным на калькуляторе расчетом и фактически полученной суммой, то не стесняйтесь написать об этом. За время своего существования калькулятор помог выявить несколько случаев банковских ошибок.

---

Последние статьи о вкладах

Последние статьи о кредитах

Последние статьи о займах

Калькулятор онлайн — Калькулятор процентов. Сложные проценты. Депозитный калькулятор

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Понятие о проценте

Проценты — одно из понятий прикладной математики, которые часто встречаются в повседневной жизни. Так, часто можно прочитать или услышать, что, например, в выборах приняли участие 56,3% избирателей, рейтинг победителя конкурса равен 74%, промышленное производство увеличилось на 3,2%, банк начисляет 8% годовых, молоко содержит 1,5% жира, ткань содержит 100% хлопка и т.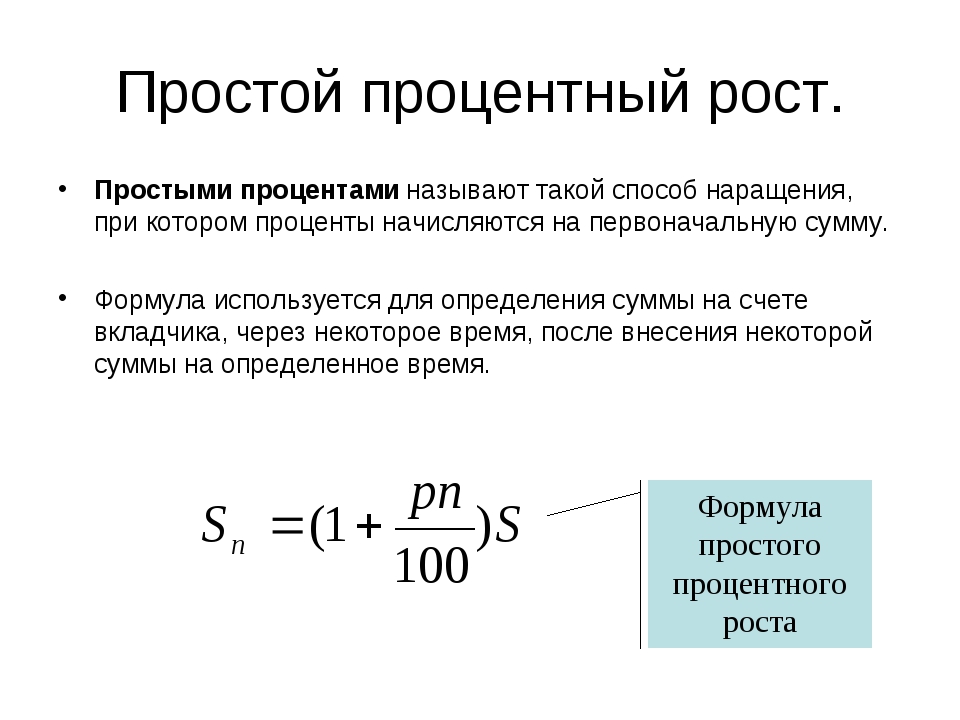 д. Ясно, что понимание такой информации необходимо в современном обществе.

Одним процентом от любой величины — денежной суммы, числа учащихся школы и т.д. — называется одна сотая ее часть. Обозначается процент знаком %, Таким образом,
1% — это 0,01, или \( \frac{1}{100} \) часть величины

Приведем примеры:
— 1% от минимальной заработной платы 2300 р. (сентябрь 2007 г.) — это 2300/100 = 23 рубля;
— 1% от населения России, равного примерно 145 млн. человек (2007 г.), — это 1,45 млн. человек;
— 3%-я концентрация раствора соли — это 3 г соли в 100 г раствора (напомним, что концентрация раствора — это часть, которую составляет масса растворенного вещества от массы всего раствора).

Понятно, что вся рассматриваемая величина составляет 100 сотых, или 100% от самой себя. Поэтому, например, надпись на этикетке «хлопок 100%» означает, что ткань состоит из чистого хлопка, а стопроцентная успеваемость означает, что в классе нет неуспевающих учеников.

Слово «процент» происходит от латинского pro centum, означающего «от сотни» или «на 100». Это словосочетание можно встретить и в современной речи. Например, говорят: «Из каждых 100 участников лотереи 7 участников получили призы». Если понимать это выражение буквально, то это утверждение, разумеется, неверно: ясно, что можно выбрать 100 человек, участвующих в лотерее и не получивших призы. В действительности точный смысл этого выражения состоит в том, что призы получили 7% участников лотереи, и именно такое понимание соответствует происхождению слова «процент»: 7% — это 7 из 100, 7 человек из 100 человек.

Знак «%» получил распространение в конце XVII века. В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «с/о» за дробь и напечатал «%». Так из-за опечатки этот знак вошел в обиход.

Любое число процентов можно записать в виде десятичной дроби, выражающей часть величины.

Чтобы выразить проценты числом, нужно количество процентов разделить на 100. Например:

\( 58\% = \frac{58}{100} = 0,58; \;\;\; 4,5\% = \frac{4,5}{100} = 0,045; \;\;\; 200\% = \frac{200}{100} = 2 \)

Для обратного перехода выполняется обратное действие. Таким образом, чтобы выразить число в процентах, надо его умножить на 100:

\( 0,58 = (0,58 \cdot 100)\% = 58\% \) \( 0,045 = (0,045 \cdot 100)\% = 4,5\% \)

В практической жизни полезно понимать связь между простейшими значениями процентов и соответствующими дробями: половина — 50%, четверть — 25%, три четверти — 75%, пятая часть — 20%, три пятых — 60% и т.д.

Полезно также понимать разные формы выражения одного и того же изменения величины, сформулированные без процентов и с помощью процентов. Например, в сообщениях «Минимальная заработная плата повышена с февраля на 50%» и «Минимальная заработная плата повышена с февраля в 1,5 раз» говорится об одном и том же. Точно так же увеличить в 2 раза — это значит увеличить на 100%, увеличить в 3 раза — это значит увеличить на 200%, уменьшить в 2 раза — это значит уменьшить на 50%.

Аналогично
— увеличить на 300% — это значит увеличить в 4 раза,
— уменьшить на 80% — это значит уменьшить в 5 раз.

Задачи на проценты

Поскольку проценты можно выразить дробями, то задачи на проценты являются, по существу, теми же задачами на дроби. В простейших задачах на проценты некоторая величина а принимается за 100% («целое»), а ее часть b выражается числом p%.

В зависимости от того, что неизвестно — а, b или р, выделяются три типа задач на проценты. Эти задачи решаются так же, как и соответствующие задачи на дроби, но перед их решением число р% выражается дробью.

1. Нахождение процента от числа.
Чтобы найти \( \frac{p}{100} \) от a, надо a умножить на \( \frac{p}{100} \):

\( b = a \cdot \frac{p}{100} \)

Итак, чтобы найти р% от числа, надо это число умножить на дробь \( \frac{p}{100} \). Например, 20% от 45 кг равны 45 • 0,2 = 9 кг, а 118% от х равны 1,18x

2. Нахождение числа по его проценту.
Чтобы найти число по его части b, выраженной дробью \( \frac{p}{100} , \; (p \neq 0) \), надо b разделить на \( \frac{p}{100} \):
\( a = b : \frac{p}{100} \)

Таким образом, чтобы найти число по его части, составляющей р% этого числа, надо эту часть разделить на \( \frac{p}{100} \). Например, если 8% длины отрезка составляют 2,4 см, то длина всего отрезка равна 2,4:0,08 = 240:8 = 30 см.

3. Нахождение процентного отношения двух чисел.
Чтобы найти, сколько процентов число b составляет от а \( (a \neq 0) \), надо сначала узнать, какую часть b составляет от а, а затем эту часть выразить в процентах:

\( p = \frac{b}{a} \cdot 100\% \) Значит, чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат умножить на 100.
Например, 9 г соли в растворе массой 180 г составляют \( \frac{9 \cdot 100}{180} = 5\% \) раствора.

Частное двух чисел, выраженное в процентах, называется процентным отношением этих чисел. Поэтому последнее правило называют правилом нахождения процентного отношения двух чисел.

Нетрудно заметить, что формулы

\( b = a \cdot \frac{p}{100}, \;\; a = b : \frac{p}{100}, \;\; p = \frac{b}{a} \cdot 100\% \;\; (a,b,p \neq 0 ) \) взаимосвязаны, а именно, две последние формулы получаются из первой, если выразить из нее значения a и p. Поэтому первую формулу считают основной и называют формулой процентов. Формула процентов объединяет все три типа задач на дроби, и, при желании, можно ею пользоваться, чтобы найти любую из неизвестных величин a, b и p.

Составные задачи на проценты решаются аналогично задачам на дроби.

Простой процентный рост

Когда человек не вносит своевременную плату за квартиру, на него налагается штраф, который называется «пеня» (от латинского роеnа — наказание).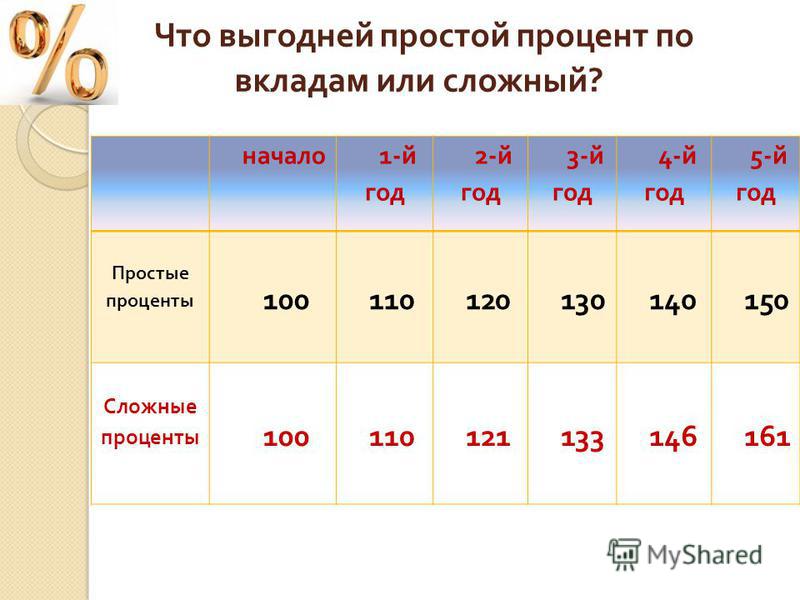 Так, если пеня составляет 0,1% от суммы квартплаты за каждый день просрочки, то, например, за 19 дней просрочки сумма составит 1,9% от суммы квартплаты. Поэтому вместе, скажем, с 1000 р. квартплаты человек должен будет внести пеню 1000 • 0,019 = 19 р., а всего 1019 р.

Ясно, что в разных городах и у разных людей квартплата, размер пени и время просрочки разные. Поэтому имеет смысл составить общую формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.

Пусть S — ежемесячная квартплата, пеня составляет р% квартплаты за каждый день просрочки, а n — число просроченных дней. Сумму, которую должен заплатить человек после n дней просрочки, обозначим S_n.
Тогда за n дней просрочки пеня составит рn% от S, или \( \frac{pn}{100}S \), а всего придется заплатить \( S + \frac{pn}{100}S = \left( 1+ \frac{pn}{100} \right) S \)
Таким образом:
\( S_n = \left( 1+ \frac{pn}{100} \right) S \)

Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.

Аналогичная формула получится, если некоторая величина уменьшается за данный период времени на определенное число процентов. Как и выше, нетрудно убедиться, что в этом случае
\( S_n = \left( 1- \frac{pn}{100} \right) S \)

Эта формула также называется формулой простого процентного роста, хотя заданная величина в действительности убывает. Рост в этом случае «отрицательный».

Сложный процентный рост

В банках России для некоторых видов вкладов (так называемых срочных вкладов, которые нельзя взять раньше, чем через определенный договором срок, например, через год) принята следующая система выплаты доходов: за первый год нахождения внесенной суммы на счете доход составляет, например, 10% от нее. В конце года вкладчик может забрать из банка вложенные деньги и заработанный доход - «проценты», как его обычно называют.

Если же вкладчик этого не сделал, то проценты присоединяются к начальному вкладу (капитализируются), и поэтому в конце следующего года 10% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.

Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк 1000 р. и ни разу в течение трех лет не будет брать деньги со счета.

10% от 1000 р. составляют 0,1 • 1000 = 100 р., следовательно, через год на его счете будет
1000 + 100 = 1100 (р.)

10% от новой суммы 1100 р. составляют 0,1 • 1100 = 110 р., следовательно, через 2 года на его счете будет
1100 + 110 = 1210 (р.)

10% от новой суммы 1210 р. составляют 0,1 • 1210 = 121 р., следовательно, через 3 года на его счете будет
1210 + 121 = 1331 (р.)

Нетрудно представить себе, сколько при таком непосредственном, «лобовом» подсчете понадобилось бы времени для нахождения суммы вклада через 20 лет. Между тем подсчет можно вести значительно проще.

А именно, через год начальная сумма увеличится на 10%, то есть составит 110% от начальной, или, другими словами, увеличится в 1,1 раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 10%. Следовательно, через 2 года начальная сумма увеличится в 1,1 • 1,1 = 1,1² раз.

Еще через один год и эта сумма увеличится в 1,1 раза, так что начальная сумма увеличится в 1,1 • 1,1² = 1,1³ раз. При таком способе рассуждений получаем решение нашей задачи значительно более простое: 1,1³ • 1000 = 1,331 • 1000 — 1331 (р.)

Решим теперь эту задачу в общем виде. Пусть банк начисляет доход в размере р% годовых, внесенная сумма равна S р., а сумма, которая будет на счете через n лет, равна S_n р.

Величина p% от S составляет \( \frac{p}{100}S \) р., и через год на счете окажется сумма
\( S_1 = S+ \frac{p}{100}S = \left( 1+ \frac{p}{100} \right)S \)
то есть начальная сумма увеличится в \( 1+ \frac{p}{100} \) раз.

За следующий год сумма S₁ увеличится во столько же раз, и поэтому через два года на счете будет сумма
\( S_2 = \left( 1+ \frac{p}{100} \right)S_1 = \left( 1+ \frac{p}{100} \right) \left( 1+ \frac{p}{100} \right)S = \left( 1+ \frac{p}{100} \right)^2 S \)

Аналогично \( S_3 = \left( 1+ \frac{p}{100} \right)^3 S \) и т.n S \)

Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.

Калькулятор сложных процентов — NerdWallet

Вот как использовать калькулятор сложных процентов NerdWallet:

• Введите начальный депозит.
• Затем введите целевой ежемесячный или годовой взнос — скажем, 100 долларов. Вы также можете ввести 0 долларов.
• При каждом вводе следите за автоматическим изменением суммы будущего баланса. Это показывает, насколько ваши сбережения и инвестиции могут со временем вырасти.
• Калькулятор учитывает начальный депозит, взносы, временной интервал, норму прибыли и частоту сложения.Вставьте разные значения, чтобы увидеть, как изменения этих цифр могут повлиять на ваш будущий баланс.

Достаточно ли вы экономите? Сравните высокодоходные сберегательные счета для получения лучших ставок.

Как работают сложные проценты

Сложные проценты просты: это проценты, которые вы зарабатываете как на свой первоначальный депозит, так и на проценты, полученные на ваши деньги. Сложный процент позволяет вашим сбережениям со временем расти быстрее.

В аккаунте, на котором выплачиваются проценты, прибыль обычно добавляется к первоначальной основной сумме в конце каждого периода начисления сложных процентов.Часто это ежедневно или ежемесячно. Каждый раз, когда проценты рассчитываются и добавляются к счету, больший баланс приводит к большему заработку процентов, чем раньше. Вот что подразумевается под сложным процентом. Обратите внимание, что на сберегательных счетах с высокой процентной ставкой деньги зарабатываются быстрее, чем на счетах с более низкой доходностью. (Найдите высокие ставки среди текущих, сберегательных и других типов счетов в списке депозитных счетов с высокими процентами NerdWallet).

Чтобы получить простое и быстрое объяснение, см. Что такое сложный процент?

Суммарный доход от инвестиций

Когда вы инвестируете в фондовый рынок, вы не получаете фиксированную процентную ставку.Вместо этого доход зависит от изменения стоимости ваших инвестиций. Когда стоимость ваших инвестиций возрастает, вы получаете прибыль.

Если вы оставляете свои деньги и прибыль, которую вы зарабатываете, инвестированной на рынке, эта прибыль со временем увеличивается так же, как и проценты.

Доходность инвестиций будет меняться из года в год и даже изо дня в день. В краткосрочной перспективе такие инвестиции, как акции или паевые инвестиционные фонды, могут фактически обесцениться.Но в долгосрочной перспективе история показывает, что диверсифицированный портфель роста может приносить в среднем от 6% до 7% в год.

Сложные проценты могут помочь в достижении ваших долгосрочных сбережений и инвестиционных целей, особенно если вы позволите им работать в течение нескольких десятилетий.

»Готовы начать зарабатывать сложные проценты? Ознакомьтесь со списком лучших сберегательных счетов NerdWallet.

Другие калькуляторы NerdWallet

Определение сложных процентов, формула, расчет

Что такое сложный процент?

Сложные проценты (или сложные проценты) — это проценты по ссуде или депозиту, рассчитываемые как на основе первоначальной основной суммы, так и накопленных процентов за предыдущие периоды.Считается, что сложный процент возник в Италии 17-го века, сложный процент можно рассматривать как «процент на процент», и он заставляет сумму расти быстрее, чем простой процент, который рассчитывается только на основную сумму.

Ставка, по которой начисляются сложные проценты, зависит от частоты начисления сложных процентов, так что чем больше количество периодов начисления сложных процентов, тем больше сложный процент. Таким образом, сумма сложных процентов, начисленных на 100 долларов США с начислением 10% годовых, будет ниже, чем сумма сложных процентов на 100 долларов США с начислением 5% годовых в течение того же периода времени.Поскольку эффект процентной ставки может приносить все более положительную прибыль на основе первоначальной основной суммы, ее иногда называют «чудом сложных процентов».

Ключевые выводы

• Сложные проценты (или сложные проценты) — это проценты, начисляемые на первоначальную основную сумму, которая также включает все накопленные проценты за предыдущие периоды по депозиту или ссуде.
• Сложный процент рассчитывается путем умножения первоначальной основной суммы на единицу плюс годовая процентная ставка, повышенная до количества составных периодов минус один.
• Проценты могут начисляться по любому заданному графику периодичности, от непрерывного до ежедневного или ежегодного.
• При расчете сложных процентов количество периодов начисления сложных процентов имеет большое значение.

Общие сведения о сложных процентах

Расчет сложных процентов

Сложные проценты рассчитываются путем умножения первоначальной основной суммы на единицу плюс годовая процентная ставка, повышенная на количество составных периодов минус один.Затем из полученной стоимости вычитается общая начальная сумма ссуды.

Кэти Керпель {Copyright} Investopedia, 2019.

Формула расчета сложных процентов:

• Сложные проценты = общая сумма основного долга и процентов в будущем (или будущая стоимость) за вычетом основной суммы в настоящее время (или приведенной стоимости)

= [P (1 + i ) ⁿ ] — P

= P [(1 + i ) ⁿ — 1]

Где:

P = основной

i = номинальная годовая процентная ставка в процентах

n = количество периодов начисления сложных процентов

Возьмите трехлетний заем в размере 10 000 долларов США под 5% годовых.Какая будет сумма процентов? В этом случае это будет:

10 000 долл. США [(1 + 0,05) ³ — 1] = 10 000 [1,157625 — 1] = 1 576,25 доллара

Рост сложных процентов

Используя приведенный выше пример (поскольку сложные проценты также учитывают накопленные проценты за предыдущие периоды), сумма процентов не будет одинаковой для всех трех лет, как это было бы с простыми процентами. Хотя общая сумма процентов, подлежащих уплате за трехлетний период по этой ссуде, составляет 1 576 долларов.25, проценты, подлежащие выплате в конце каждого года, показаны в таблице ниже.

Периоды начисления

При расчете сложных процентов количество периодов начисления сложных процентов имеет большое значение. Основное правило состоит в том, что чем больше количество периодов начисления сложных процентов, тем больше сумма сложных процентов.

Следующая таблица демонстрирует разницу, которую может составить количество периодов начисления сложных процентов для ссуды в размере 10 000 долларов США с годовой процентной ставкой 10% в течение 10-летнего периода.

Сложные проценты могут значительно повысить доходность инвестиций в долгосрочной перспективе. В то время как вклад в размере 100 000 долларов, который получает 5% простых годовых процентов, принесет 50 000 долларов в общей сумме процентов за 10 лет, годовые сложные проценты в размере 5% на 10 000 долларов составят 62 889,46 долларов за тот же период. Если бы период начисления сложных процентов вместо этого выплачивался ежемесячно в течение того же 10-летнего периода под 5% сложных процентов, общая сумма процентов вырастала бы до 64 700,95 долларов.

Расчет компаундирования в Excel

Если с тех пор, как вы учились в математике, прошло некоторое время, не бойтесь: есть удобные инструменты для вычисления сложного слова.Многие калькуляторы (как карманные, так и компьютерные) имеют функции экспоненты, которые вы можете использовать для этих целей. Если возникают более сложные сложные задачи, вы можете выполнить их в Microsoft Excel тремя различными способами.

1. Первый способ расчета сложных процентов — это умножение нового баланса каждого года на процентную ставку. Предположим, вы вкладываете 1000 долларов на сберегательный счет с годовой процентной ставкой 5% и хотите рассчитать остаток через пять лет.В Microsoft Excel введите «Год» в ячейку A1 и «Баланс» в ячейку B1. Введите годы от 0 до 5 в ячейки с A2 по A7. Баланс за год 0 составляет 1000 долларов, поэтому вы должны ввести «1000» в ячейку B2. Затем введите «= B2 * 1,05» в ячейку B3. Затем введите «= B3 * 1.05» в ячейку B4 и продолжайте делать это, пока не дойдете до ячейки B7. В ячейке B7 вычисление будет «= B6 * 1,05». Наконец, вычисленное значение в ячейке B7 — 1276,28 доллара — это остаток на вашем сберегательном счете через пять лет. Чтобы найти значение сложных процентов, вычтите 1000 долларов из 1276 долларов.n) — P. »В третьей строке модуля введите« Конечная функция ». Вы создали макрос функции для расчета сложной процентной ставки. Продолжая с той же таблицы Excel выше, введите« Сложный процент »в ячейку A6 и введите «= Compound_Interest (B1, B2, B3).» Это даст вам значение 276,28 доллара США, что согласуется с первыми двумя значениями.

Использование других калькуляторов

Как упоминалось выше, в Интернете предлагается ряд бесплатных калькуляторов сложных процентов, и многие портативные калькуляторы также могут выполнять эти задачи.

• Бесплатный калькулятор сложных процентов, предлагаемый на сайте Financial-Calculators.com, прост в использовании и предлагает выбор частоты сложных процентов от дня до года. Он включает в себя возможность выбора непрерывного начисления процентов, а также позволяет вводить фактические календарные даты начала и окончания. После ввода необходимых данных расчета результаты показывают заработанные проценты, будущую стоимость, годовую процентную доходность (APY), которая является мерой, включающей начисление сложных процентов и ежедневные проценты.
• Investor.gov, веб-сайт, управляемый Комиссией по ценным бумагам и биржам США (SEC), предлагает бесплатный онлайн-калькулятор сложных процентов. Калькулятор довольно прост, но он позволяет вводить ежемесячные дополнительные депозиты основному лицу, что полезно для расчета доходов, когда вкладываются дополнительные ежемесячные сбережения.
• Бесплатный онлайн-калькулятор процентов с несколькими дополнительными функциями доступен на TheCalculatorSite.com. Этот калькулятор позволяет производить расчеты для различных валют, учитывать ежемесячные депозиты или снятия, а также автоматически рассчитывать ежемесячные депозиты или снятия с поправкой на инфляцию.

Частота смешивания

Проценты могут быть увеличены по любому заданному графику периодичности, от ежедневного до ежегодного. Существуют стандартные графики частоты начисления сложных процентов, которые обычно применяются к финансовым инструментам.

Обычно для сберегательных счетов в банках используется ежедневный график начисления сложных процентов. Для компакт-диска типичные графики частоты начисления сложных процентов — ежедневно, ежемесячно или раз в полгода; для счетов денежного рынка — часто ежедневно. Для жилищных ипотечных ссуд, ссуд под залог недвижимости, ссуд для личного бизнеса или счетов по кредитным картам обычно применяется ежемесячный график начисления сложных процентов.

Также могут быть разные временные рамки, в течение которых начисленные проценты фактически зачисляются на существующий баланс. Проценты по счету могут начисляться ежедневно, но только ежемесячно. Только когда проценты фактически зачисляются или добавляются к существующему балансу, они начинают приносить дополнительные проценты на счет.

Некоторые банки также предлагают так называемое непрерывное начисление сложных процентов, которое в любой момент увеличивает проценты к основной сумме долга.С практической точки зрения, это не намного больше, чем ежедневное начисление сложных процентов, если вы не хотите вкладывать деньги и снимать их в тот же день.

Более частое начисление сложных процентов выгодно инвестору или кредитору. Для заемщика все наоборот.

Временная стоимость денег Возмещение

Понимание временной стоимости денег и экспоненциального роста, создаваемого сложным капиталом, важно для инвесторов, стремящихся оптимизировать свои доходы и распределение богатства.

Формула для получения будущей стоимости (FV) и текущей стоимости (PV) выглядит следующим образом:

FV = PV (1 + i) ⁿ и PV = FV / (1 + i) ⁿ

Например, будущая стоимость 10 000 долларов США составит 5% годовых в течение трех лет:

= 10 000 долл. США (1 + 0,05) ³

= 10 000 долл. США (1 157 625 долл. США)

= 11 576,25 долл. США

Приведенная стоимость 11 576,25 долларов США со скидкой 5% на три года:

= 11 576 долларов США.25 / (1 + 0,05) ³

= 11 576,25 долл. США / 1 157 625 долл. США

= 10 000 долл. США

Обратное значение 1,157625, равное 0,8638376, в данном случае является коэффициентом дисконтирования.

Рассмотрение по «Правилу 72»

Так называемое Правило 72 рассчитывает приблизительное время, в течение которого инвестиции удвоятся при заданной норме прибыли или процентах «i», и определяется выражением (72 / i). Его можно использовать только для годовой рецептуры.

Например, инвестиция с годовой доходностью 6% удвоится через 12 лет.Таким образом, инвестиции с годовой доходностью 8% за девять лет увеличатся вдвое.

Совокупный годовой темп роста (CAGR)

Совокупный годовой темп роста (CAGR) используется для большинства финансовых приложений, которые требуют расчета единого темпа роста за период времени.

Допустим, ваш инвестиционный портфель вырос с 10 000 до 16 000 долларов за пять лет; что такое CAGR? По сути, это означает, что PV = — 10 000 долларов США, FV = 16 000 долларов США и nt = 5, поэтому переменная «i» должна быть вычислена.Используя финансовый калькулятор или Excel, можно показать, что i = 9,86%.

Согласно соглашению о движении денежных средств, ваши первоначальные инвестиции (PV) в размере 10 000 долларов США отображаются с отрицательным знаком, поскольку они представляют собой отток средств. Чтобы найти «i» в приведенном выше уравнении, PV и FV обязательно должны иметь противоположные знаки.

CAGR Реальные приложения

CAGR широко используется для расчета доходности за периоды времени для акций, паевых инвестиционных фондов и инвестиционных портфелей.CAGR также используется для определения того, превышал ли управляющий паевым инвестиционным фондом или управляющий портфелем рыночную норму прибыли в течение определенного периода времени. Если, например, рыночный индекс обеспечил общую доходность 10% за пятилетний период, но управляющий фондом получил только 9% годовой прибыли за тот же период, это означает, что управляющий отстал от рынка.

CAGR также можно использовать для расчета ожидаемых темпов роста инвестиционных портфелей в течение длительных периодов времени, что полезно для таких целей, как накопление средств на пенсию.Рассмотрим следующие примеры:

Пример 1: Не склонный к риску инвестор доволен скромной 3% годовой доходностью своего портфеля. Таким образом, ее нынешний портфель в 100 000 долларов через 20 лет вырастет до 180 611 долларов. Напротив, толерантный к риску инвестор, который ожидает годовой доходности 6% от своего портфеля, через 20 лет увидит, что 100 000 долларов вырастут до 320 714 долларов.

Пример 2: CAGR можно использовать для оценки того, сколько нужно убрать, чтобы сэкономить для конкретной цели.Пара, которая хотела бы сэкономить 50 000 долларов в течение 10 лет на первоначальный взнос за кондоминиум, должна будет экономить 4 165 долларов в год, если они предполагают, что годовая прибыль (CAGR) составит 4% от своих сбережений. Если они готовы пойти на небольшой дополнительный риск и рассчитывать на среднегодовой темп роста 5%, им нужно будет экономить 3 975 долларов в год.

Пример 3: CAGR также может продемонстрировать преимущества инвестирования в более раннем, чем в более позднем возрасте. Если цель состоит в том, чтобы сэкономить 1 миллион долларов до выхода на пенсию в возрасте 65 лет, исходя из среднегодового роста в 6%, 25-летнему человеку нужно будет откладывать 6 462 доллара в год для достижения этой цели.С другой стороны, 40-летнему человеку нужно будет сэкономить 18 227 долларов, или почти в три раза больше, чтобы достичь той же цели.

• CAGR также часто встречается в экономических данных. Вот пример: ВВП на душу населения в Китае увеличился с 193 долларов в 1980 году до 6091 долларов в 2012 году. Каков годовой рост ВВП на душу населения за этот 32-летний период? Темп роста «i» в данном случае составляет впечатляющие 11,4%.

Плюсы и минусы компаундирования

Хотя магия компаундирования привела к апокрифической истории Альберта Эйнштейна, назвавшего его восьмым чудом света или величайшим изобретением человека, компаундирование также может работать против потребителей, у которых есть ссуды с очень высокими процентными ставками, например, задолженность по кредитной карте.Баланс кредитной карты в размере 20 000 долларов США с ежемесячной процентной ставкой 20% приведет к общей сумме сложных процентов в размере 4 388 долларов США за год или около 365 долларов США в месяц.

С положительной стороны, магия начисления сложных процентов может работать вам на пользу, когда дело касается ваших инвестиций, и может быть мощным фактором создания богатства. Экспоненциальный рост за счет сложных процентов также важен для смягчения факторов, разрушающих благосостояние, таких как рост стоимости жизни, инфляция и снижение покупательной способности.

Паевые инвестиционные фонды предлагают инвесторам один из самых простых способов воспользоваться преимуществами сложных процентов. Решение реинвестировать дивиденды, полученные от паевого инвестиционного фонда, приводит к покупке большего количества акций фонда. Со временем накапливается больше сложных процентов, и цикл покупки большего количества акций будет продолжать способствовать росту стоимости инвестиций в фонд.

Рассмотрим инвестиционный паевой инвестиционный фонд, открытый с начальными 5000 долларов и ежегодным приростом в 2400 долларов. При средней годовой доходности 12% за 30 лет будущая стоимость фонда составляет 798 500 долларов.Сложный процент — это разница между денежными средствами, внесенными в инвестицию, и фактической будущей стоимостью инвестиции. В этом случае за счет внесения 77 000 долларов США или совокупного взноса в размере всего 200 долларов США в месяц в течение 30 лет сложные проценты составляют 721 500 долларов США будущего баланса.

Конечно, доходы от сложных процентов подлежат налогообложению, если только деньги не находятся на счете, защищенном от налогов; обычно он облагается налогом по стандартной ставке, установленной для налоговой категории налогоплательщика.

Инвестиции со сложными процентами

Инвестор, который выбирает план реинвестирования в рамках брокерского счета, по сути, использует возможность начисления сложных процентов во все, что он инвестирует. Инвесторы также могут получить сложный процент при покупке облигации с нулевым купоном. Традиционные выпуски облигаций обеспечивают инвесторам периодические выплаты процентов на основе первоначальных условий выпуска облигаций, и, поскольку они выплачиваются инвестору в форме чека, проценты не складываются.

Бескупонные облигации не высылают инвесторам процентные чеки; вместо этого облигации этого типа приобретаются со скидкой по сравнению с их первоначальной стоимостью и со временем растут. Эмитенты бескупонных облигаций используют возможность начисления сложных процентов для увеличения стоимости облигации, чтобы она достигла своей полной цены к моменту погашения.

Компаундирование также может работать на вас при выплате кредита. Например, если вы будете выплачивать половину ипотечного кредита дважды в месяц вместо того, чтобы вносить полный платеж один раз в месяц, это сократит ваш период амортизации и сэкономит вам значительную сумму процентов.

Кстати о займах…

Сообщение о начислении процентов

Закон о правде в кредитовании (TILA) требует, чтобы кредиторы раскрывали условия кредита потенциальным заемщикам, включая общую сумму процентов в долларах, подлежащую выплате в течение срока действия кредита, а также то, начисляются ли проценты простым или сложным образом.

Другой метод — сравнить процентную ставку по ссуде с ее годовой процентной ставкой (APR), которую TILA также требует от кредиторов. Годовая процентная ставка конвертирует финансовые расходы по вашему кредиту, которые включают все проценты и комиссии, в простую процентную ставку.Существенная разница между процентной ставкой и годовой процентной ставкой означает один или оба из двух сценариев: в вашем ссуде используются сложные проценты или в дополнение к процентам он включает огромные комиссии по ссуде. Даже когда речь идет о ссуде одного и того же типа, диапазон годовых может сильно различаться между кредиторами в зависимости от комиссий финансового учреждения и других расходов.

Вы заметите, что процентная ставка, которую вы взимаете, также зависит от вашего кредита. Ссуды, предлагаемые тем, у кого хорошая кредитная история, имеют значительно более низкие процентные ставки, чем те, которые взимаются с заемщиков с плохой кредитной историей.

Часто задаваемые вопросы

Какое простое определение сложных процентов?

Сложные проценты относятся к явлению, при котором проценты, связанные с банковским счетом, ссудой или инвестициями, со временем растут экспоненциально, а не линейно. Ключом к пониманию концепции является слово «составной». Предположим, вы инвестируете 100 долларов в бизнес, который ежегодно выплачивает вам 10% дивидендов. У вас есть выбор: вложить эти дивиденды в наличные или реинвестировать эти выплаты в дополнительные акции.Если вы выберете второй вариант, реинвестируя дивиденды и сложив их вместе с вашими первоначальными инвестициями в 100 долларов, то получаемая вами прибыль со временем начнет расти.

Кому выгодны сложные проценты?

Проще говоря, сложные проценты приносят пользу инвесторам, но значение слова «инвесторы» может быть довольно широким. Банки, например, получают выгоду от сложных процентов, когда ссужают деньги и реинвестируют полученные проценты в выдачу дополнительных ссуд.Вкладчики также извлекают выгоду из сложных процентов, когда они получают проценты по своим банковским счетам, облигациям или другим инвестициям. Важно отметить, что, хотя термин «сложные проценты» включает слово «проценты», эта концепция применяется за пределами ситуаций, для которых обычно используется слово «проценты», таких как банковские счета и ссуды.

Могут ли сложные проценты сделать вас богатым?

Да. Фактически, сложные проценты, возможно, являются самой мощной из когда-либо задуманных сил для создания богатства.Есть записи о купцах, кредиторах и различных бизнесменах, которые использовали сложные проценты, чтобы разбогатеть буквально на тысячи лет. Например, в древнем городе Вавилон глиняные таблички использовались более 4000 лет назад для обучения студентов математике сложных процентов.

В наше время Уоррен Баффет стал одним из самых богатых людей в мире благодаря бизнес-стратегии, которая включала в себя старательно и терпеливо увеличивать доходность его инвестиций в течение длительных периодов времени.Вполне вероятно, что в той или иной форме люди будут использовать сложные проценты для создания богатства в обозримом будущем.

Страница не найдена

• Образование

  • Общий

    • Словарь
    • Экономика
    • Корпоративные финансы
    • Рот ИРА
    • Акции
    • Паевые инвестиционные фонды
    • ETFs
    • 401 (к)

  • Инвестирование / Торговля

    • Основы инвестирования
    • Фундаментальный анализ
    • Управление портфелем ценных бумаг
    • Основы трейдинга
    • Технический анализ
    • Управление рисками
• Рынки

  • Новости

    • Новости компании
    • Новости рынков
    • Торговые новости
    • Политические новости
    • Тенденции

  • Популярные акции

    • Яблоко (AAPL)
    • Тесла (TSLA)
    • Amazon (AMZN)
    • AMD (AMD)
    • Facebook (FB)
    • Netflix (NFLX)
• Симулятор
• Твои деньги

  • Личные финансы

    • Управление благосостоянием
    • Бюджетирование / экономия
    • Банковское дело
    • Кредитные карты
    • Домовладение
    • Пенсионное планирование
    • Налоги
    • Страхование

  • Обзоры и рейтинги

    • Лучшие онлайн-брокеры
    • Лучшие сберегательные счета
    • Лучшие домашние гарантии
    • Лучшие кредитные карты
    • Лучшие личные займы
    • Лучшие студенческие ссуды
    • Лучшее страхование жизни
    • Лучшее автострахование
• Советники

  • Ваша практика

    • Управление практикой
    • Продолжая образование
    • Карьера финансового консультанта
    • Инвестопедия 100

  • Управление благосостоянием

    • Портфолио Строительство
    • Финансовое планирование
• Академия

  • Популярные курсы

    • Инвестирование для начинающих
    • Станьте дневным трейдером
    • Торговля для начинающих
    • Технический анализ

  • Курсы по темам

    • Все курсы
    • Торговые курсы
    • Курсы инвестирования
    • Финансовые профессиональные курсы

Представлять на рассмотрение

Извините, страница, которую вы ищете, недоступна.Вы можете найти то, что ищете, используя наше меню или параметры поиска.

дом

• О нас
• Условия эксплуатации
• Словарь
• Редакционная политика
• Рекламировать
• Новости
• Политика конфиденциальности
• Свяжитесь с нами
• Карьера
• Уведомление о конфиденциальности Калифорнии

• #
• А
• B
• C
• D
• E
• F
• грамм
• ЧАС
• я
• J
• K
• L
• M
• N
• О
• п
• Q
• р
• S
• Т
• U
• V
• W
• Икс
• Y
• Z

Investopedia является частью издательской семьи Dotdash.

Простой процент против сложного процента

Простой процент против сложного процента: обзор

Проценты — это стоимость заимствования денег, когда заемщик платит кредитору комиссию за ссуду. Проценты, обычно выражаемые в процентах, могут быть простыми или сложными. Простой процент основан на основной сумме кредита или депозита. Напротив, сложные проценты основаны на основной сумме и процентах, которые накапливаются по ней за каждый период.Простые проценты начисляются только на основную сумму кредита или депозита, поэтому их легче определить, чем сложные проценты.

Ключевые выводы

• Проценты — это стоимость заимствования денег, когда заемщик платит кредитору комиссию за ссуду.
• Как правило, простые проценты, выплачиваемые или полученные в течение определенного периода, представляют собой фиксированный процент от основной суммы, которая была заимствована или предоставлена ​​в ссуду.
• Сложные проценты начисляются и добавляются к накопленным процентам за предыдущие периоды, поэтому заемщики должны уплачивать проценты по процентам, а также основную сумму долга.

Простые проценты

Простой процент рассчитывается по следующей формуле:

Взаимодействие с другими людьми Простой интерес знак равно п × р × п где: п знак равно Основная сумма р знак равно Годовая процентная ставка п знак равно Срок кредита, лет \ begin {align} & \ text {Simple Interest} = P \ times r \ times n \\ & \ textbf {где:} \\ & P = \ text {Основная сумма} \\ & r = \ text {Годовая процентная ставка} \\ & n = \ text {Срок кредита, в годах} \\ \ end {выровнен} Простой процент = P × r × n, где: P = основная сумма r = годовая процентная ставка = срок кредита в годах

Как правило, простые проценты, выплачиваемые или полученные в течение определенного периода, представляют собой фиксированный процент от основной суммы, которая была заимствована или ссужена.Например, предположим, что студент получает ссуду с простой процентной ставкой для оплаты одного года обучения в колледже, которое стоит 18000 долларов, а годовая процентная ставка по ссуде составляет 6%. Студент погашает ссуду в течение трех лет. Выплачиваемая сумма простых процентов составляет:

Взаимодействие с другими людьми $ 3 , 2 4 0 знак равно $ 1 8 , 0 0 0 × 0 . 0 6 × 3 \ begin {align} & \ $ 3,240 = \ 18 000 $ \ times 0,06 \ times 3 \\ \ end {align} 3240 долларов = 18000 долларов × 0,06 × 3

а общая выплаченная сумма составляет:

Взаимодействие с другими людьми $ 2 1 , 2 4 0 знак равно $ 1 8 , 0 0 0 + $ 3 , 2 4 0 \ begin {align} & \ 21 240 долларов = \ 18 000 долларов США + \ 3 240 долларов США \\ \ end {align} 21 240 долл. США = 18 000 долл. США + 3 240 долл. США

Сложные проценты

Сложные проценты начисляются и добавляются к накопленным процентам за предыдущие периоды; Другими словами, он включает проценты по процентам.t — P \\ & \ textbf {где:} \\ & P = \ text {Основная сумма} \\ & r = \ text {Годовая процентная ставка} \\ & t = \ text {Применяется процентная ставка за количество лет} \\ \ конец {выровнен} Сложные проценты = P × (1 + r) t − P, где: P = основная сумма r = годовая процентная ставка t = количество лет, на которые начисляются проценты

Он рассчитывается путем умножения основной суммы на единицу плюс годовая процентная ставка, повышенная на количество сложных периодов, а затем минус уменьшение основной суммы за этот год.В случае сложных процентов заемщики должны выплачивать проценты как на проценты, так и на основную сумму.

Примеры простых и сложных процентов

Ниже приведены несколько примеров простых и сложных процентов.

Пример 1

Предположим, вы вложили 5000 долларов в годовой депозитный сертификат (CD), по которому выплачиваются простые проценты под 3% годовых. Процент, который вы заработаете через год, составит 150 долларов:

Взаимодействие с другими людьми $ 5 , 0 0 0 × 3 % × 1 \ начало {выровнено} & \ 5 000 $ \ times 3 \% \ times 1 \\ \ end {выровнено} 5000 долларов США × 3% × 1

Пример 2

Продолжая приведенный выше пример, предположим, что ваш депозитный сертификат можно обналичить в любое время, при этом проценты выплачиваются вам пропорционально.Если вы обналичите компакт-диск через четыре месяца, сколько вы заработаете в виде процентов? Вы получите 50 долларов: $ 5 , 0 0 0 × 3 % × 4 1 2 \ begin {выровнено} & \ 5 000 $ \ times 3 \% \ times \ frac {4} {12} \\ \ end {выровнено} 5000 долларов США × 3% × 124

Пример 3

Предположим, Боб занимает 500 000 долларов на три года у своего богатого дяди, который соглашается взимать с Боба простые проценты под 5% годовых. Сколько Бобу придется выплачивать проценты каждый год и каковы будут его общие проценты через три года? (Предположим, что основная сумма останется неизменной в течение трех лет, т.е.д., полная сумма кредита будет выплачена через три года.) Бобу придется платить 25000 долларов в качестве процентов каждый год:

Взаимодействие с другими людьми $ 5 0 0 , 0 0 0 × 5 % × 1 \ begin {выровнен} & \ 500 000 $ \ times 5 \% \ times 1 \\ \ end {выровнен} 500 000 долларов США × 5% × 1

или 75 000 долларов США в виде процентов по истечении трех лет:

Взаимодействие с другими людьми $ 2 5 , 0 0 0 × 3 \ begin {align} & \ 25 000 $ \ times 3 \\ \ end {align} 25 000 долл. США × 3

Пример 4

Продолжая приведенный выше пример, Бобу необходимо дополнительно занять 500 000 долларов на три года.К сожалению, его богатый дядя отключен. Таким образом, он берет ссуду в банке по процентной ставке 5% годовых, начисляемых ежегодно, с полной суммой ссуды и выплатой процентов через три года. Какой будет общий процент, выплачиваемый Бобом?

Поскольку сложные проценты рассчитываются на основе основной суммы и накопленных процентов, вот как они складываются:

Взаимодействие с другими людьми После первого года выплаты процентов знак равно $ 2 5 , 0 0 0 , или же $ 5 0 0 , 0 0 0 (Основная сумма займа) × 5 % × 1 После второго года выплата процентов знак равно $ 2 6 , 2 5 0 , или же $ 5 2 5 , 0 0 0 (Основная сумма займа + проценты за первый год) × 5 % × 1 После третьего года выплата процентов знак равно $ 2 7 , 5 6 2 .5 0 , или же $ 5 5 1 , 2 5 0 Основная сумма займа + проценты за первый год и два) × 5 % × 1 Общая сумма процентов к уплате через три года знак равно $ 7 8 , 8 1 2 . 5 0 , или же $ 2 5 , 0 0 0 + $ 2 6 , 2 5 0 + $ 2 7 , 5 6 2 . 5 0 \ begin {align} & \ text {После первого года, выплата процентов} = \ 25 000 долларов США \ text {,} \\ & \ text {или} \ 500 000 долларов США \ text {(Основная сумма займа)} \ times 5 \% \ times 1 \\ & \ text {После второго года выплата процентов} = \ 26 250 долларов \ text {,} \\ & \ text {или} \ 525 000 долларов \ text {(основная сумма кредита + проценты за первый год)} \\ & \ times 5 \ % \ times 1 \\ & \ text {После третьего года, выплата процентов} = \ 27 562 доллара США.50 \ text {,} \\ & \ text {или} \ $ 551 250 \ text {Основная сумма займа + проценты за первый год} \\ & \ text {и два)} \ times 5 \% \ times 1 \\ & \ text {Общая сумма процентов к уплате через три года} = \ 78 812,50 долларов США \ text {,} \\ & \ text {или} \ 25 000 долларов США + \ 26 250 долларов США + \ 27 562,50 долларов США \\ \ end {выровнено} После первого года проценты к уплате = 25000 долларов США или 500000 долларов США (основная сумма кредита) × 5% × 1 После второго года подлежащие выплате проценты = 26 250 долларов США или 525000 долларов США (основная сумма кредита + проценты первого года) × 5% × 1 После третьего года процентные выплаты = 27 562,50 долларов США или 551 250 долларов США по основной сумме кредита + проценты за первый и второй годы) × 5% × 1 Общая сумма процентов, подлежащих выплате через три года = 78 812 долларов США.3 — \ 500 000 долл. США \\ \ end {выровнено} Общая сумма процентов, подлежащих уплате через три года = 78 812,50 долларов США или 500 000 долларов США (основная сумма кредита) × (1 + 0,05) 3 — 500 000 долларов США

Этот пример показывает, как формула для сложных процентов возникает из выплаты процентов по процентам, а также основной суммы.

Что такое сложный процент?

Сложные проценты — важная концепция, которую необходимо понимать при управлении своими финансами. Это может помочь вам получить более высокую прибыль от ваших сбережений и инвестиций, но также может работать против вас, когда вы платите проценты по ссуде.

Узнайте, как работают сложные проценты, как они рассчитываются и как воспользоваться этой простой, но феноменальной концепцией, чтобы максимизировать свои инвестиции.

Определение и примеры сложных процентов

Подумайте о сложных процентах как о том, что происходит, когда возникает «эффект снежного кома». Снежок начинается с малого, но чем больше добавляется снега, тем больше он становится. По мере роста он становится больше и быстрее.

Сложные проценты — это проценты, полученные от первоначальной основной суммы плюс накопленные проценты.Вы не только получаете проценты по своему начальному депозиту, но и получаете проценты по процентам.

Как работает сложный процент?

Чтобы понять сложные проценты, начните с концепции простых процентов: вы вкладываете деньги, а банк выплачивает вам проценты по вашему депозиту.

Например, если вы зарабатываете 5% годовых, депозит в размере 100 долларов принесет вам 5 долларов через год. Что произойдет в следующем году? Вот тут-то и появляется сложное начисление. Вы будете получать проценты на свой первоначальный депозит, и вы будете получать проценты на только что заработанные проценты.

Процент, полученный вашими деньгами на второй год, будет больше, чем годом ранее, потому что баланс вашего счета теперь составляет 105 долларов, а не 100 долларов.

Со сложными процентами, даже если вы не вносите никаких дополнительных вкладов, ваш заработок возрастет.

• Первый год: Первоначальный депозит в размере 100 долларов приносит 5% годовых, или 5 долларов, в результате чего ваш баланс достигает 105 долларов.
• Год второй: Ваши 105 долларов приносят 5% годовых, или 5,25 доллара. Ваш баланс составляет 110,25 доллара США.
• Год третий: Ваш баланс 110,25 доллара приносит 5% годовых, или 5,51 доллара. Ваш баланс увеличивается до 115,76 долларов США.

Выше приведен пример годового начисления процентов. Во многих банках, в том числе в онлайн-банках, проценты ежедневно накапливаются и добавляются на ваш счет ежемесячно, поэтому процесс продвигается еще быстрее.

Конечно, если вы занимаете деньги, начисление сложных процентов работает против вас и в пользу вашего кредитора. Вы платите проценты на взятые взаймы деньги.В следующем месяце, если вы не выплатили всю сумму своей задолженности, вы должны будете выплатить проценты на взятую вами сумму плюс начисленные проценты.

Как рассчитать сложный процент?

Вы можете рассчитать сложные проценты несколькими способами. Если вы научитесь делать это самостоятельно, то сможете получить ценную информацию о том, как достичь своих целей по сбережениям, сохраняя при этом реалистичные ожидания. Каждый раз, когда вы проводите расчеты, исследуйте несколько сценариев «что, если», используя разные числа, и посмотрите, что произойдет, если вы сэкономите немного больше или заработаете проценты еще на несколько лет.

Онлайн-калькуляторы

работают лучше всего, так как они делают математические вычисления за вас и могут легко создавать диаграммы и годовые таблицы.

Некоторые люди предпочитают смотреть на числа более подробно, выполняя расчеты самостоятельно. Вы можете использовать финансовый калькулятор с функциями хранения формул или обычный калькулятор с ключом для вычисления показателей.

Используйте следующую формулу для расчета сложных процентов:

Чтобы использовать этот расчет, введите следующие переменные:

• A: — это сумма , с которой вы в итоге получите.
• P: Ваш первоначальный депозит, известный как основная сумма .
• r: годовая процентная ставка , записана в десятичном формате.
• n: число периодов начисления сложных процентов в год (например, ежемесячно — 12, а еженедельно — 52).
• t: сумма времени (в годах), через которую складываются ваши деньги.

Делаем математику

У вас есть 1000 долларов США, зарабатывающих 5% ежемесячно.(180)

А = 1000 (2,113703)

А = 2113,70

Через 15 лет у вас будет примерно 2114 долларов. Ваше окончательное число может незначительно отличаться из-за округления. Из этой суммы 1000 долларов США представляют собой ваш первоначальный депозит, а оставшиеся 1114 долларов США — это проценты.

Образец электронной таблицы в Документах Google показывает, как это работает. Также есть загружаемая копия для использования с вашими номерами.

Использование электронных таблиц

Таблицы могут сделать за вас весь расчет.Чтобы рассчитать окончательный баланс после начисления сложных процентов, вы обычно используете расчет будущего значения . Microsoft Excel, Google Таблицы и другие программные продукты предлагают эту функцию, но вам нужно будет немного изменить числа.

Используя приведенный выше пример, вы можете выполнить расчет с помощью функции будущей стоимости Excel:

Введите каждую из ваших переменных в отдельные ячейки. Например, в ячейке A1 может быть «1000», чтобы представить ваш первоначальный депозит, а в ячейке B1 может быть «15», чтобы представить 15 лет.

Уловка использования электронной таблицы для сложных процентов состоит в том, чтобы использовать сложение периодов вместо того, чтобы просто думать годами. Для ежемесячного начисления сложных процентов периодическая процентная ставка — это просто годовая ставка, деленная на 12, потому что в году 12 месяцев или «периодов». Для ежедневного начисления сложных процентов большинство организаций используют 360 или 365.

1. = FV (ставка, кпер, пт, пв, тип)
2. = FV ([. 05/12], [15 * 12], 1000,)

В этом примере исключен раздел pmt , который будет периодическим добавлением к учетной записи.Если бы вы добавляли деньги на счет ежемесячно, это пригодилось бы. Тип в этом случае также не используется. Вы могли бы использовать это, если хотите произвести расчет в зависимости от срока платежа.

Правило 72

Правило 72 — еще один способ быстро оценить сложные проценты. Этот метод может дать вам приблизительную оценку того, сколько времени потребуется, чтобы удвоить ваши деньги, исходя из процентной ставки и продолжительности времени, в течение которого вы заработаете эту ставку.Умножьте количество лет на процентную ставку. Если у вас 72, у вас есть комбинация факторов, которые примерно удвоят ваши деньги.

Пример 1: У вас есть сбережения в размере 1000 долларов США, приносящие 5% годовых, или «годовой процентный доход». Сколько времени потребуется, чтобы на вашем счету было 2000 долларов?

Чтобы найти ответ, выясните, как получить 72. Поскольку 72 разделенное на 5 дает 14,4, потребуется около 14,4 лет, чтобы удвоить ваши деньги.

Пример 2: Сейчас у вас есть 1000 долларов, а через 20 лет вам понадобятся 2000 долларов.Какую ставку вы должны заработать как минимум, чтобы к тому времени ваши деньги удвоились?

Опять же, выясните, что нужно, чтобы добраться до 72, используя имеющуюся у вас информацию, в данном случае это количество лет. Поскольку 72 разделенные на 20 равняются 3,6, вам нужно будет заработать примерно 3,6% годовых, чтобы достичь своей цели за этот период времени.

Что это значит для индивидуальных инвесторов и вкладчиков

Как индивидуальный вкладчик и, возможно, даже инвестор, есть способы убедиться, что начисление сложных процентов работает в вашу пользу.

Экономьте раньше и чаще

Когда вы увеличиваете свои сбережения, время — ваш друг. Чем дольше вы можете оставлять свои деньги нетронутыми, тем больше они могут расти, потому что сложные проценты со временем увеличивают деньги в геометрической прогрессии.

Если вы вносите 100 долларов в месяц под 5% годовых с начислением ежемесячных процентов в течение пяти лет, вы сэкономите 6000 долларов на депозитах и ​​заработаете 800,61 доллара в виде процентов. Даже если вы больше никогда не внесете депозит по истечении этого времени, через 20 лет на вашем счету будет заработано дополнительно 7 573 доллара.87 процентов — намного больше, чем ваши начальные $ 6000 на депозитах, благодаря начислению сложных процентов.

Проверьте APY

Чтобы сравнить банковские продукты, такие как сберегательные счета и компакт-диски, посмотрите на годовую процентную доходность. Он учитывает начисление сложных процентов и обеспечивает истинную годовую ставку. Банки обычно публикуют APY, поскольку он выше процентной ставки. Вам следует попытаться получить приличные ставки по своим сбережениям, но, вероятно, не стоит менять банк еще на 0,10%, если у вас нет очень большого остатка на счете.

Быстро погасить долги и доплатить, когда сможешь

Оплата только минимальной суммы по кредитной карте обойдется вам дорого. Вы вряд ли уменьшите процентные платежи, и ваш баланс действительно может вырасти. Если у вас есть студенческие ссуды, не капитализируйте проценты (добавляя невыплаченные проценты к общей сумме остатка) и платите хотя бы проценты по мере их накопления, чтобы не получить неприятный сюрприз после окончания учебы. Даже если вы не обязаны платить, вы окажете себе услугу, сведя к минимуму свои пожизненные процентные расходы.

Сохраняйте низкие ставки заимствования

Помимо влияния на ваш ежемесячный платеж, процентные ставки по вашим кредитам определяют, насколько быстро ваш долг будет расти и сколько времени потребуется для его погашения. Трудно бороться с двузначными ставками, которые есть у большинства кредитных карт. Посмотрите, имеет ли смысл консолидировать долги и снизить процентные ставки, пока вы выплачиваете долги; это может ускорить процесс и сэкономить ваши деньги.

Что делает сложные проценты сильными?

При повторной выплате процентов происходит начисление процентов.Первые один или два цикла не особенно впечатляют, но все начинает улучшаться после того, как вы снова и снова добавляете интерес.

Частота

Частота сложения имеет значение. Более частые периоды начисления сложных процентов — например, ежедневно — дают более впечатляющие результаты. При открытии сберегательного счета ищите счета, которые увеличиваются ежедневно. Вы можете видеть, что процентные платежи добавляются к вашему счету только ежемесячно, но расчеты по-прежнему можно производить ежедневно. Некоторые счета начисляют проценты только ежемесячно или ежегодно.

Время

Компаундирование более драматично в течение длительных периодов времени. Опять же, у вас есть большее количество вычислений или «кредитов» на счет, когда деньги остаются в покое, чтобы расти.

Процентная ставка

Процентная ставка также является важным фактором баланса вашего счета с течением времени. Более высокие ставки означают, что счет будет расти быстрее, но сложные проценты могут преодолеть более низкую ставку. Особенно в течение длительных периодов времени на счете с более низкой ставкой сложный баланс может оказаться более высоким, чем на счете, использующем простой расчет.Посчитайте, произойдет ли это, и найдите точку безубыточности.

Вклады

Снятие и депозиты также могут повлиять на баланс вашего счета. Лучше всего подойдет рост ваших денег или регулярное добавление новых депозитов на ваш счет. Если вы снимаете свои доходы, вы ослабляете эффект начисления сложных процентов.

Начальная сумма

Сумма денег, с которой вы начинаете, не влияет на начисление процентов. Независимо от того, начинаете ли вы со 100 или 1 миллиона долларов, сложное начисление работает одинаково.Результаты кажутся больше, когда вы начинаете с большого депозита, но вас не наказывают за то, что вы начинаете с малого или ведете отдельные счета. Лучше всего сосредоточиться на процентах и ​​времени при планировании своего будущего: какой процент вы будете зарабатывать и как долго? Доллары — это всего лишь результат вашей ставки и временных рамок.

Ключевые выводы

• При использовании сложных процентов вы получаете проценты по уже полученным процентам
  .
• Во многих банках процентные ставки ежедневно увеличиваются, что позволяет
  быстрее приумножить свои деньги.
• Онлайн-калькуляторы позволяют легко вычислить сложные проценты.
• Экономьте раньше, чтобы получить максимальную прибыль.

Что такое сложный процент? | Банковская ставка

Сложные проценты — мощная сила для людей, которые хотят увеличить свои сбережения. Вот почему понимание того, как это работает — и как это использовать — очень важно.

Определение сложных процентов

Когда вы вкладываете деньги на сберегательный или аналогичный счет, вы обычно получаете проценты в зависимости от внесенной вами суммы.Например, если вы поместите 1000 долларов на счет, на который выплачивается 1 процент годовых, вы получите 10 долларов процентов через год.

Сложные проценты — это проценты, которые вы зарабатываете на проценты. Итак, в приведенном выше примере на второй год вы заработаете 1 процент от 1010 долларов, или 10,10 доллара на выплату процентов. Сложные проценты ускоряют ваш процентный доход, помогая быстрее расти вашим сбережениям. Со временем вы будете получать проценты по постоянно растущим остаткам на счетах, которые выросли за счет процентов, полученных в предыдущие годы.В долгосрочной перспективе сложные проценты могут привести к очень быстрому росту ваших процентных доходов и помочь вам построить богатство.

По многим банковским счетам, например сберегательным счетам и счетам денежного рынка, а также по инвестициям начисляются проценты. Как вкладчик или инвестор вы получаете процентные платежи по заранее установленному графику, например, ежедневно, ежемесячно, ежеквартально или ежегодно. А депозиты на этих счетах будут увеличивать процент, который вы зарабатываете, выплачивая дополнительные проценты на уже заработанные проценты.

В зависимости от счета проценты могут начисляться по разным графикам. Например, на базовом сберегательном счете могут начисляться сложные проценты ежедневно, еженедельно или ежемесячно.

Как работают сложные проценты?

Важно отметить, что график начисления сложных процентов и выплаты процентов может отличаться. Например, сберегательный счет может выплачивать проценты ежемесячно, но ежедневно увеличивать их. Каждый день банк будет рассчитывать ваш процентный доход на основе остатка на счете плюс проценты, которые вы заработали, но не выплачены.

Чем выше процентная ставка по счету и чем чаще начисляются сложные проценты, тем больше процентов вы будете получать за определенный период времени. Чтобы проиллюстрировать, как работает начисление сложных процентов, ниже мы включили формулу начисления сложных процентов, а также несколько примеров того, как начисление сложных процентов влияет на прибыль.

Формула сложных процентов:

Начальный баланс * (1 + (процентная ставка / количество начислений за период) ^{количество начислений за период * количество периодов}

Чтобы увидеть, как работает формула рассмотрим этот пример.

У вас есть 100 000 долларов на двух разных сберегательных счетах, на каждый из которых выплачивается 2 процента годовых. На одном счете начисляются проценты ежегодно, а на другом — ежедневно. Вы ждете один год и снимаете деньги с обоих счетов.

С первого счета, на который начисляются проценты только раз в год, вы получите:

100 000 долларов США * (1 + (0,02 / 1) ^{1 * 1} = 102 000 долларов США

на второй счет, на котором начисляются проценты каждый день, вы получите:

100000 долларов США * (1 + (.02/365) ^{365 * 1} = 102020,08 доллара США

Поскольку процент, который вы зарабатываете каждый день во втором примере, также приносит проценты в последующие дни, вы зарабатываете на 20,08 доллара больше, чем на счете, который увеличивает проценты на ежегодной основе.

В долгосрочной перспективе влияние сложных процентов становится больше, потому что вы получаете проценты на большие остатки на счетах, которые возникли в результате многолетнего получения процентов по предыдущим процентным доходам.Если, например, вы оставили свои деньги на счете на тридцать лет, то конечное сальдо будет выглядеть следующим образом.

Для годового начисления:

100000 долларов США * (1 + (.02 / 1) ^{1 * 30} = 181136,16 долларов США

Для ежедневного начисления сложных процентов:

100000 долларов США * (1 + (.02 / 365) ^{365 * 30} = 182 208,88 долларов США

За 30-летний период всю работу за вас сделали сложные проценты. Первоначальный депозит в размере 100 000 долларов почти удвоился.В зависимости от того, как часто ваши деньги накапливались, баланс вашего счета вырос до более чем 181 000 долларов США или 182 000 долларов США.

И ежедневное начисление сложных процентов принесло вам дополнительные 1072,72 доллара, или более 35 долларов в год.

Процентная ставка, которую вы зарабатываете на свои деньги, также оказывает большое влияние на эффективность начисления сложных процентов. Если бы по сберегательному счету выплачивалось 5 процентов в год вместо 2 процентов, конечные остатки были бы такими:

	1 год	30 лет
Годовое начисление	105 000 долл. США	432 194 долл. США.24
Суточная рецептура	$ 105 126,75	448 122,87 долл. США

Чем выше процентная ставка, тем больше разница между конечным сальдо в зависимости от частоты начисления сложных процентов.

Наш калькулятор сложных процентов поможет вам рассчитать, сколько процентов вы будете получать с разных счетов.

Как воспользоваться сложными процентами

Есть несколько способов, которыми обычные люди могут воспользоваться сложными процентами.

1. Ранняя экономия

Сила начисления сложных процентов приходит от времени. Чем дольше вы оставляете деньги на сберегательном счете или инвестируете в рынок, тем больше процентов на них будет начисляться. Чем больше времени ваши деньги остаются на счете, тем больше может происходить начисление сложных процентов, а это означает, что вы можете получать дополнительные проценты на заработанные проценты.

Рассмотрим пример человека, который откладывает 10 000 долларов в год в течение 10 лет, а затем прекращает экономить, по сравнению с человеком, который откладывает 2,500 долларов в год в течение 40 лет.Если предположить, что оба человека зарабатывают 7% годовых, усугубляемых ежедневно, по прошествии 40 лет у них будет следующая сумма.

Экономия 10 000 долларов в год в течение 10 лет, а затем ничего в течение 30 лет	Экономия 2,500 долларов в год в течение 40 лет	Экономия 5000 долларов в год в течение 40 лет
1 182 470,57 долл. США	$ 551 542,64	$ 1 103 085,27

Оба человека откладывают одну и ту же общую сумму в 100 000 долларов, но человек, который раньше откладывал больше, в конце 40 лет получает гораздо больше.Даже тот, кто экономит 200000 долларов, или вдвое больше за полные 40 лет, в итоге получает меньше, потому что он распределяет свои сбережения на 40 лет вместо того, чтобы делать большую часть своих сбережений заранее.

2. Проверьте APY

Чем выше процентная ставка по счету, тем больше процентов вы получите от денег, которые вы положили на счет, и тем больше сложных процентов вы заработаете. В то время как простая процентная ставка — хороший показатель для использования, годовая процентная доходность (APY) — лучший показатель, на который стоит обратить внимание.

APY показывает эффективную процентную ставку счета, включая все начисления сложных процентов. Если вы поместите 1000 долларов на счет, на который выплачивается 1 процент годовых, через год вы можете получить более 1010 долларов на счете, если проценты будут составлять более одного года.

Если в аккаунте рекламируется APY в размере 1%, по прошествии года на вашем счете будет ровно 1010 долларов, потому что APY учитывает начисление сложных процентов.

Сравнение APY, а не процентной ставки двух счетов покажет, какой действительно приносит больше процентов.

3. Проверьте частоту начисления сложных процентов

Сравнивая счета, не смотрите только на APY. Посмотрите, как часто они составляют проценты. Чем чаще они объединяются, тем лучше. При сравнении двух счетов с одинаковой процентной ставкой, тот, у которого более частое начисление сложных процентов, будет иметь более высокий APY, что означает, что он будет выплачивать больше процентов на один и тот же остаток на счете.

Подробнее:

Сложные проценты и почему это важно

Сложные проценты, которые часто называют «восьмым чудом света», позволяют вашим деньгам работать на вас.

Что такое сложные проценты?

Сложные проценты — это проценты по депозиту, рассчитываемые как на основе первоначальной основной суммы, так и накопленных процентов за предыдущие периоды. [1] Или, проще говоря, сложные проценты — это проценты, которые вы зарабатываете на проценты. Вы можете начислять проценты по разным частотным графикам, например, ежедневно, ежемесячно или ежегодно.

Чем больше количество периодов начисления сложных процентов, тем больше начисленные проценты.Думайте об этом как о снежном коме. Чем раньше вы начнете экономить и чем больше денег вы добавите в свой снежный ком, тем крупнее он станет. А теперь подумайте, толкнули ли вы снежный ком с заснеженного холма. Теперь снег, который вы уже уложили, останется, и вы накопите больше снега. В конце концов, когда ваш снежок достигнет подножия холма, он будет содержать снег, с которого вы начали, снег, который он собрал по пути, и даже больше снега поверх него.

Другими словами, эффект процентной ставки может генерировать постоянно увеличивающуюся прибыль в зависимости от вашей первоначальной суммы инвестиций.Таким образом, чем чаще вы откладываете и чем больше сумма сбережений, тем больший процент будет получен. Это также называют «чудом сложных процентов».

Почему важны сложные проценты?

Сложные проценты ускоряют рост вашего богатства. Это заставляет денежную сумму расти более быстрыми темпами, чем простой процент, потому что вы будете получать прибыль от вложенных денег, а также от прибыли в конце каждого периода начисления сложных процентов. Это означает, что вам не нужно откладывать столько денег, чтобы достичь своих целей!

Магия начисления сложных процентов может быть важным фактором при увеличении вашего богатства.Чем раньше вы откроете процентный счет и начнете накапливать деньги, тем больше денег вы заработаете в виде сложных процентов. Это также ключ к смягчению последствий разрушающих благосостояние факторов, таких как рост стоимости жизни, инфляция и снижение покупательной способности.

Как рассчитать сложные проценты:

Сложные проценты рассчитываются путем умножения первоначальной основной суммы на единицу плюс годовая процентная ставка, увеличенная до количества составных периодов, минус один.

При расчете сложных процентов количество периодов начисления сложных процентов имеет большое значение. Чем больше количество периодов начисления сложных процентов, тем больше сложный процент.

Сделайте это проще — используйте этот калькулятор для расчета сложных процентов!

Обязательно проконсультируйтесь со своим налоговым или финансовым консультантом о том, как лучше всего начать работу. Как всегда, мы здесь, чтобы помочь! Свяжитесь с нами или посетите ваш местный центральный банк с любыми вопросами.

Источники:

[1] Сложный процент, Investopedia

.